- #1
Speedking96
- 104
- 0
Homework Statement
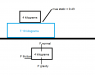
Two masses M1 = 4.00 kg and M2 = 7.10 kg are stacked on top of each other as shown in the figure. The static coefficient of friction between M1 and M2 is μs = 0.430. There is no friction between M2 and the surface below it.
What is the maximum horizontal force that can be applied to M2 without M1 sliding relative to M2?
Homework Equations
F=ma
Ffriction = μFnormal
The Attempt at a Solution
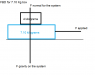
For the 4 kg box:
Fnet = ma
Ff=ma
μmg = ma
μg=a
(0.43)(9.81) = a = 4.23 m/s/s
I understand that this must be the acceleration for the whole system, but when I calculate the max force, do I do it for the whole system's mass or for the 7.10 kg box only? Why or why not?