Block sliding down a ramp

[EchoTheCat]

Homework Statement

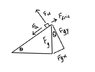
A block with a mass of 820 g starts from rest at the top of an inclined plane that is 106 cm long and makes an angle of 49.5 degrees with the horizontal. It accelerates uniformly down the ramp and reaches the bottom in 0.89 s. What is the coefficient of kinetic friction on the ramp?

Homework Equations

x=v_ot +0.5at²
u_k = F_k/N

The Attempt at a Solution

In order to calculate coefficient of friction, I need the normal force and F_k.
vo = 0 (starts at rest)
x = 106 cm = 1.06 m
t = 0.89 sec
a = ?
1.06 = 0.5(0.89 ²)(a)
a = 2.67643 m/s/s
Then, Fk = (2.67643 m/s/s)(0.82 kg) = 2.1947 N
N = (0.82 kg) (9.8 m/s/s) cos 49.5 degrees = 5.219 N
2.1947/5.219 = 0.421

 

[RedDelicious]

a = 2.67643 m/s/s
Then, Fk = (2.67643 m/s/s)(0.82 kg) = 2.1947 N

You're going to want to rethink this. The net force was friction? Where is gravity in all of this?

 

[Chandra Prayaga]

Draw a diagram and show all the forces on the block. That is always the correct starting point.

 

[EchoTheCat]

You're going to want to rethink this. The net force was friction? Where is gravity in all of this?

The vertical component of gravity is 0.82*9.8*cos 49.5 degrees = 5.219
The horizontal component of gravity would be 0.82*9.8*sin 49.5 degrees = 6.1106.
So, Fx(net) = 6.1106 - 2.1947 = 3.9159 ?
And uf = 3.9159/5.219 = 0.750 ?

 

[PeroK]

The vertical component of gravity is 0.82*9.8*cos 49.5 degrees = 5.219
The horizontal component of gravity would be 0.82*9.8*sin 49.5 degrees = 6.1106.
So, Fx(net) = 6.1106 - 2.1947 = 3.9159 ?
And uf = 3.9159/5.219 = 0.750 ?

You perhaps mean the normal and tangential components of gravity. Think this through:

You calculated the acceleration.

What can you work out immediately from this? Hint: think of Newton's laws.

 

[EchoTheCat]

You perhaps mean the normal and tangential components of gravity. Think this through:

You calculated the acceleration.

What can you work out immediately from this? Hint: think of Newton's laws.

I don't think I understand what you're saying.

Mass is given as 0.82 kg, and I calculated acceleration to be 2.67642. So then force would be 2.195.

 

[Chandra Prayaga]

As PeroK says: You should always start from first principles. If you draw the diagram, you will know what are all the forces acting on the object. Then you can write Newton's law. Then you can define a coordinate system, take components, and then look for the unknowns.
Incidentally, your use of the words "vertical" and "horizontal" is not corect. You should refer to a coordinate system which you define< in this case, as an axis parallel to the inclined plane and one perpendicular to the inclined plane (again, diagram!).

 

[EchoTheCat]

theta = 49.5 degrees
Fg = (0.82 kg) (9.8 m/s/s) = 8.036 N
Fn = Fgy = Fg cos 49.5 degrees = 8.306*cos 49.5 degrees = 5.219 N
Fa = 2.67643 m/s/s * 0.82 kg = 2.195 N
Fgx = Fg * sin 49.5 degrees = 6.1106 N

 

[Chandra Prayaga]

Good. So, what is Newton's second law?

 

[EchoTheCat]

net force = mass x acceleration

 

[PeroK]

net force = mass x acceleration

Okay, so first you calculated the acceleration. From that you got the total net force.

Now, what forces are acting on the block? In fact, you have those in your diagram. So, which force do you need to calculate now?

 

[EchoTheCat]

I need to calculate Fk, the force of kinetic friction.

 

[PeroK]

I need to calculate Fk, the force of kinetic friction.

So, how do you do that? Think about what forces you already know.

 

[EchoTheCat]

Wouldn't Fk = Fgx - Fa = 6.1106 - 2.195 = 3.9156 N?

 

[PeroK]

Wouldn't Fk = Fgx - Fa = 6.1106 - 2.195 = 3.9156 N?

If $F_a$ is the net force, then that is correct.

Finally, how do you get the coefficient of friction from the frictional force?

 

[EchoTheCat]

3.9159/5.219 = 0.750

 

[PeroK]

3.9159/5.219 = 0.750

Well, those are three numbers. But what are they?

 

[EchoTheCat]

Fk = 3.9159
Fn = 5.219
uf = Fk/Fn = 3.9159/5.219 = 0.750

 

[PeroK]

Fk = 3.9159
Fn = 5.219
uf = Fk/Fn = 3.9159/5.219 = 0.750

The method looks right. I haven't checked the numbers, though.

PS $\mu = 0.75$ looks right!

You can only really give the answer to two decimal places.