- #1
mattg443
- 12
- 0
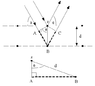
I am aware that when an X ray is 'reflected' from the sheets of a crystal lattice, some radiation passes through whilst remaining radiation penetrates different layers or is scattered.
And that if the path difference of the wave traveled is an integral value of wavelengths, constructive interference occurs
However, my problem is, that in all the diagrams, I don't see how interference could occur, because the waves are in two distinct locations, therefore, not interfering at all.
E.g in the attachment, the wave that is reflected of the second layer cannot interfere with the wave reflected off the first layer.
Is this just an oversimplification of the diagram, or a flaw in my understanding?
Thanks!
And that if the path difference of the wave traveled is an integral value of wavelengths, constructive interference occurs
However, my problem is, that in all the diagrams, I don't see how interference could occur, because the waves are in two distinct locations, therefore, not interfering at all.
E.g in the attachment, the wave that is reflected of the second layer cannot interfere with the wave reflected off the first layer.
Is this just an oversimplification of the diagram, or a flaw in my understanding?
Thanks!