BRS: Exploring the Rubik Group with GAP

[Chris Hillman]

[size=+]I. Introduction[/size]

With great sadness I note the passing of one of the Best Things Ever: a few days ago, John Baez posted the final installment (Week 300) in his long-running internet column, This Week's Finds in Mathematical Physics.

But John himself is not sad; he is desperate--- to save the world. See Week 300 for his own explanation, and note that his various blogs and writings will continue, but focusing on extra-mathematical topics.

What does this have to do with the Rubik cube? Well, the topic of Week 300 happens to be very closely related to one of my own interests, the theory of "combinatorial species", a subject created by Andre Joyal using the notions of category theory. One way to try to briefly encapsulate what this theory is all about is to say that an old and often reinvented idea in mathematics involves working with "points" which have been endowed with some kind of "structure", and then two fundamental problems are:

• how do you count "structured points"?
• how do you permute "structured points"?

The basic idea is to encode some family of "structured sets", such as "finite ternary trees", as a certain functor. Then we obtain a number of generating functions, having very nice formal properties, including far-reaching generalizations of zeta functions and the counting polynomials used in the theory of Polya enumeration.

The theory of "combinatorial species" forms part of the background needed to appreciate another major but under-reported recent event: a group of researchers claimed to have established (via computer) that in the Rubik group (the symmetry group of the 3x3x3 Rubik cube), every element can be expressed in terms of the six standard generators and their inverses using at most 20 words in the "face turn metric", which counts $f, f^2, f^3 = f^{-1}$ as one face turn, where $f$ is a clockwise quarter-turn of the front face (in a standard notation due to Singmaster). I wrote "claimed to have established" because the work has not yet been published, but the authors are leaders in this field and have previously published papers on the same topic, so there is a very good chance their claim is correct.

As I write, the Wikipedia articles which mention this development are not quite right, since they confuse the "face turn metric" with the "quarter turn metric" in which $f^{\pm1}$ counts as one move but $f^2$ counts as two moves. The face turn metric is closer to the experience of "cubers" manipulating a physical Rubik's cube, but the quarter-turn metric is the one which is directly related to the question: what is the diameter of the Cayley graph of the Rubik group with the six standard generators by quarter turns of the six faces $u, \, f, \, r, \, l, \, b, \,d$ (up, front, right, left, back, down). This problem has been unsolved for 30 years, since it was first asked by David Singmaster! Results about the maximal number of moves in either the face-turn or quarter-turn metric required to express elements of the Rubik group can be considered alternative ways of answering the question: how much better is "God's algorithm" for solving the Rubik cube than the algorithms used by the best human "speedcubers"?

The problems of determining the maximal shortest word in the face turn and quarter turn metrics are certainly distinct, since it has been known for some time that the "superflip" (a particular interesting element of the Rubik group) requires 20 moves in the face-turn metric (so that, according to the new result, this element belongs to the set of rather rare elements which require the maximal number of moves in the face-turn metric), but another element, "superflip with four-spot" requires more moves in the quarter-turn metric than does the superflip. AFAIK, the best current result--- it's due to Tomas Rokicki, a coauthor of the research in question--- for the quarter-turn metric is that every element of the Rubik group can be expressed using at most 29 turns in the q-turn metric. However, AFAIK, Rokicki conjectures that the diameter of the Cayley graph of the Rubik group with the six quarter-turn generators is in fact 26.

In this thread, I hope to provide some background needed to appreciate statements about the Rubik group. At the very least, I hope to provide

• a tutorial on using GAP to define and play around with the Rubik group and some related groups, including at least a sketch of how you can start working out your very own algorithm for solving the Rubik cube puzzle,
• essential (?) background:
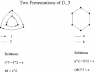
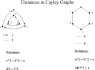
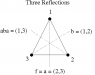
  • a brief illustrated explanation of Cayley graphs and a related concept, Schreier graphs,
  • the principle result concerning the Rubik group, the structure theorem of Ann Scott which expresses it as a specific index 12 subgroup of the group
    $$\left( C_3 \wr S_8 \right) \times \left( C_2 \wr S_{12} \right)$$
    which is the direct product of two generalized permutation groups (if you haven't seen this before, but guess it has something to do with "independent" generalized permutations of the eight "corner cubies" and the twelve "edge cubies", you guess correctly!),
  • a tutorial on wreath products--- a construction giving an answer (actually, two answers) to the question: "how do you permute structured points?"--- particularly the case of generalized symmetric groups and generalized alternating groups, including
    • a "fiber-bundle" picture related to Kleinian geometry,
    • the Frobenius cocycle and how we can use that to construct a Cayley graph from the Schreier graphs associated with a (possibly not subnormal) series of nested subgroups of G,
    • the "restoration problem" for generalized symmetric/alternating groups
  • some background on the major problems of computational group theory and how most of them can be efficiently solved,

Possible additional topics include, in no particular order:

• some background on group theory generally, particularly
  • the intuitive meaning of conjugate elements, conjugate subgroups, cosets, and commutator elements in a given group,
  • actions by a given group G and the category of G-sets, including the basic structure theorems,
  • permutation representations of groups vs. linear representations of groups,
• some background on the theory of "random permutations" drawn from a given permutation group, in particular symmetric/alternating groups and the Rubik group, plus a tutorial on using GAP to gather (reliable) statistics about possibly huge finite permutation groups,
• some background on combinatorial group theory, including generators and relations, and the problem of "translating" words expressed with respect using one generating set to an equivalent word expressed using another generating set, mentioning some fundamental and open problems for the Rubik group,
• some background on Kleinian geometry, needed to fully appreciate the "fiber-bundle" picture associated with wreath products, possibly also discussion of some small examples of finite projective spaces, affine spaces, finite analogs of euclidean geometry, etc.,
• some background on Wille's "concept theory", which applies to any relation (so very general), is easy to use and learn, and often provides useful insight, so IMO it deserves to be better known,
• since a sequence of finite constructions is often best understood in terms of a single countable construction, some background on oligomorphic permutation groups, homogeneous countable graphs and the Erdos-Renyi "universal (countable) random graph",
• some background on an information theory "unifying" Boltzmann's notion of entropy (microstates and macrostates) with Galois theory, which (given an action by a group G on a set X) answers the question: "what information is required to say how the points of a subset A of X are moved by an element g, if we know how the points of another possibly disjoint subset B are moved by g?".

To my distress, it appears to be utterly impossible for me to escape the unwelcome intrusion into every aspect of my existence of several phenomena which are, sad to say, also deeply relevant to the research in question:

• Wikipedia and its ills,
• the workings of the New Panopticon, including the public-private partnership between multinational spycos (a category in which I include Google) and secret police agencies of various states.

I don't want to talk about those aspects, and in any case the Mentors would probably discourage such discussion. But honesty compels me to mention that they are highly relevant--- although this probably won't be at all obvious unless you are already familiar with all the stuff I have mentioned in this post. PM me with your PKI public key if you cannot contain your curiosity about the alleged relevance, but let's not discuss it further here.

An ironical detail: I don't possesses a physical Rubik cube, and due to concerns about Java script, I can't access the many on-line tutorials which use Java script to describe alleged "solutions of the cube". So my knowledge of "cubing" is (so far) entirely theoretical!

 

[Chris Hillman]

BRS: Exploring the Rubik Group with GAP. II. References

[size=+]II. References.[/size]

I want to immediately provide a list of references for further reading, for those who are impatient to start learning more immediately, and as insurance against the possibility that I will not be able to say more than a small fraction of what I promised to say in the first post.

Some relevant webpages (paste these URLs into your browser's "location pane"):

• website containing the announcement of the claimed result: 20 face turns suffice:
  [PLAIN]http://www.cube20.org/
  [/PLAIN]
• some related Wikipedia articles
  
  http://en.wikipedia.org/wiki/Optimal_solutions_for_Rubik%27s_Cube
• John Baez's collected TWF posts:
  [PLAIN]http://www.math.ucr.edu/home/baez/TWF.html
  [/PLAIN]
• the GAP website:
  
  http://www.gap-system.org/
  http://www.gap-system.org/Doc/Examples/rubik.html
• the website of Peter Cameron
  
  [URL]http://www.maths.qmul.ac.uk/~pjc/[/URL]
  (lots of fun and readable expository papers on things like the Parker vector which are related to material I may discuss).

Some excellent printed books which will be very useful to anyone wishing to better understand the Rubik cube puzzle and other permutation puzzles, listed very roughly in order of decreasing utility+relevance:

• Grossman and Magnus, Groups and their Graphs; high school level (!) introduction to groups via Cayley graphs; short and readable, and very useful if you can find it!--- this book stands at the top of my list of Books I Wish Dover Would Reprint; the second author was a leader in the field of combinatorial group theory,
• Neumann, Stoy, and Thompson, Groups and Geometry, Oxford U Press, 1994: advanced ugrad level; very readable and fun, and includes a chapter on exploring the Rubik group with GAP!,
• Cameron, Permutation Groups, Cambridge U Press, 1999: advanced ugrad level, a bit less readable but extremely informative about such topics as oligomorphic permutation groups and the Erdos-Renyi graph,
• Joyner, Adventures in Group Theory, Johns Hopkins U Press, 2002: somewhat disorganized and informal, but offers lots of information on the Rubik group (alas, citations are mainly to non-peer-reviewed research published only on the "cubelover's mailing list", but stuff is probably not as unreliable as that characterization might make it sound!),
• Massey, Algebraic Topology, Springer, 1967: grad textbook on homotopy theory (no homology theory!); Appendix B offers a very short but excellent introduction to three of the four most important structure theorems in the theory of G-sets,
• Cameron, Combinatorics, Cambridge U Press, 1994: ugrad textbook, very readable, covers Polya enumeration, the Schreier-Sims algorithm (the foundation of computational group theory), Frucht's theorem, and some other relevant topics,
• Scott, Group Theory, org. publ. 1964, Dover, 1987: older but readable; Chapter 10 offers a nice account of the traditional approach to the theory of permutation groups (unfortunately not including the crucial topic of the "table of marks"; the author is W. R. Scott, not Ann Scott, don't know if they are related,
• Davey and Priestly, Introduction to Lattices and Order, Cambridge U Press, 1990: grad level, elementary material relevant to subgroup lattice of a group, subgroup lattice of a subgroup and quotient group; last chapter is an introduction to Wille's concept theory,
• Cox, Little, and O'Shea, Ideals, Varieties, and Algorithms, Springer, 1992: ugrad level, one of the five best books ever published, IMO; an introduction to computational algebraic geometry (Groebner bases and all that); Chapter 7 offers an excellent short introduction to the invariant theory of finite groups,
• James and Liebeck, Representations and Characters of Groups, Cambridge U Press, 1993: grad level, short and very readable introduction to the classical theory of linear representations of finite groups, which is so beautiful and useful that it entirely eclipsed the previous invention of Georg Frobenius, in the theory of permutation representations of finite groups, which of course includes the subject of this thread!,
• Sturmfels, Algorithms in Invariant Theory, Springer, 1993: short grad level introduction to the classical theory of the invariants of finite groups, which is an essential complement to the theory of linear representations of finite groups, and essential background for some of the material I may discuss; I highly recommend reading this book at the same time you read the textbook by James and Liebeck because linear representations and invariants are so closely connected!,
• Wilf, Generatingfunctionology, Academic Press, 1990: ugrad level; entertaining introduction to enumerative combinatorics; this is the book I once (c. 1993) tried to rewrite entirely from the viewpoint of "combinatorial species"!; excellent background for Week 300 and several other TWF postings of John Baez,
• McLarty, Elementary Categories, Elementary Toposes, Oxford U Press, 1995: grad level introduction to category theory and topos theory; the category of G-sets (for a given G) is one of the most important examples of an elementary topos; one way to informally understand this is that the entire metatheory of logic and mathematics could have been founded upon the theory of G-sets (choose your G) instead of the theory of sets; this book provides more excellent background for Week 300 and other postings in the TWF series,
• Johnson, Presentations of Groups, Cambridge U Press, 1990: grad level, nice short introduction to combinatorial group theory,
• Armstrong, Groups and Symmetry, Springer, 1988: ugrad level textbook; very readable but less directly relevant information than Neumann et al., but see the remarks on conjugate elements in geometric symmetry groups,
• Carter, Segal, and MacDonald, Lectures on Lie Groups and Lie Algebras, Cambrige U Press, 1995: grad level survey, offers sketchy but very readable brief introductions which should help interested SA/Ms to partially understand how some of the material I may discuss can be viewed as discrete analogs of phenomena in the theory of reflection groups, flag manifolds, etc.,
• Sharpe, Differential Geometry, Springer, 1997: grad level textbook on Cartanian geometry, unfortunately not very readable but offers the only modern attempt I know of to introduce Kleinian geometry; Cartanian geometry is the common generalization of Kleinian geometry and Riemannian geometry; this subject has close connections with the theory of principle fiber bundles and with "gauge theories" in physics,
• Hatcher, Algebraic Topology, Cambridge U Press, 2001: grad level textbook; very readable and inspiring; several illustrations in the chapter on homotopy theory are IMO useful for understanding generators and presentations (full disclosure: I drew them back in my undergrad days, so I'm biased).

Uhm... in case I didn't make this sufficiently clear: I intend this list as a smorgasbord from which intrigued SA/Ms can choose any item which catches their fancy; I certainly don't intend it as a list of "required background" reading for the thread or anything like that!

 

[Chris Hillman]

BRS: Exploring the Rubik Group with GAP. III. Cayley Digraphs

[size=+]III. Cayley Digraphs[/size]

The result claimed at cube20.org comes with a vivid picture involving the Cayley graph of the Rubik group (treated as permutation group generated by six specific generators, the quarter turns $f,u,r,b,d,l$). As we'll see, this graph--- strictly speaking, I should call it a digraph, since its edges are directed--- contains

• 43252003274489856000 vertices
• six directed edges entering and six directed edges leaving every vertex

That is one fairly humungous graph, so I can't really draw it--- although I can draw "homomorphic images" of it, in a sense to be explained, which graphically display some of its "coarse structure".

But here I just want to quickly give the idea of the Cayley graph associated with a group and a specific generating set, so I'll draw instead two Cayley graphs describing a much smaller group, the dihedral group having 6 elements, which is usually written $D_3$, which arises as the group of symmetries of an ordinary equilateral triangle.

First, make a paper model of a triangle and label its vertices in order 1,2,3. Now

• let $r$ denote a 1/3 clockwise rotation (in the plane) about the centroid of the triangle,
• let $f$ denote the reflection across a line drawn through any vertex and the centroid,

These two invertible linear transformations (in fact, they are euclidean isometries) take the triangle to itself, but permute the vertices and edges. You can see that they have order 3, 2 respectively, i.e. $r^3 = f^2 = e$, where $e$ is customarily used in this context to denote the identity transformation. Next, convince yourself of another law obeyed by these two transformations: $(r \, f)^2 = r \, f \, r \, f = e$, or equivalently $f \, r \, f = r^{-1}$. Furthermore, every symmetry of the triangle (every euclidean isometry taking the triangle to itself) can be expressed as the composition of r, f, so these two elements generate the symmetry group, which turns out to have six elements.

It is of course best to learn enough about combinatorial group theory to be able to prove these facts by hand. Here I just want to pause to show you very quickly how you can verify with GAP that I am not totally making this up. If you have installed GAP 4 and have started a GAP session, you should be able to type the commands shown below:

gap> G := F/[ F.1^3, F.2^2, (F.1*F.2)^2 ];
<fp group on the generators [ r, f ]>
gap> Size(G);
6
gap> IsomorphismGroups(G, DihedralGroup(6));
[ r, f ] -> [ f2, f1 ]

In this output from a GAP session, each command is preceded by the gap> prompt, and the output is shown after each command. GAP knows all about combinatorial group theory, and it knows the definition of the dihedral groups, so it has verified that indicated relations completely define the correct group up to group isomorphism. Not only that, but we have learned that GAP defines this dihedral group by the very presentation we used! (With the trivial distinction that it lists f first and r second.)

We are actually more interested in a permutation representation, however:

perms := GeneratorsOfGroup(Image(IsomorphismPermGroup(G)));
[ (1,2,3), (2,3) ]
gap> IsomorphismGroups(Group(last),G);
[ (1,2,3), (2,3) ] -> [ r, f ]

Here we instructed GAP to try to find a permutation representation, and then we asked it for an explicit isomorphism between the permutation group generated by the two permutations $(1,2,3), \, (2,3)$ and our first representation of the group, and it came up with:
$$(1,2,3) \rightarrow r, \; (2,3) \rightarrow f$$

In the last quarter of 19th century, Cayley noticed that we can obtain a vivid graphical illustration of the presentation in terms of the generators r,f; see the leftmost graph in the first and second figures below.

Two terminological notes:

• Following the convention employed by most modern algebra textbooks and also used by GAP, we are multiplying permutations left to right:
  
  gap> (2,3)*(1,2);
  (1,2,3)
  This is a good convention in part because it is consistent with the Cayley graph picture, in which we want to compose transformations by "following the arrows"; see the third figure below and verify by following the arrows that the product permutation sends
  $$1 \rightarrow 2, \; 2 \rightarrow 3, \; 3 \rightarrow 1$$
  which is what we mean by writing the three-cycle $(1,2,3)$.
• Because $f^2 = e$, we have $f^{-1} = f$; to make the Cayley digraphs easier to draw and "read", instead of drawing two directed edges we draw only one undirected edge for any generator of order two. This convention is also universal in books which use Cayley digraphs.

A fundamental feature of presentions of a group by generators and relations is that there will always be infinitely many representations of each element of the group (each transformation, in the case of a symmetry group) by various "words" in the given generators. For example, by following arrows in the leftmost graph in the second figure, you can easily verify that $r \,f \, r^2 \,f = r^2 = r^{-1}$, which gives three equivalent words for the same element of the group. In other words:

• words correspond to sequences of moves using the generating elements
• each element can be obtained by infinitely many such sequences

And this last feature is the entire point of the result about the Rubik group which is claimed in cube20.org: some words are dramatically shorter than others, and for a given generating set, we want to compute the shortest word representing each element of the group. Textbooks on combinatorial group theory will tell you how to do this, but one obvious prerequisite is that you must have a presentation of the group of interest, in terms of the generating set of interest! And it turns out that this is another problem concerning the Rubik group which has been unsolved for 30 years (see Joyner).

To clarify: of course we know the generators, and we certainly know some relations they obey, what we don't know are certain unknown relations among the generators, which we would need to obtain a presentation of the Rubik group!

(If we simply omit some of the relations needed, we'll obtain a presentation of some completely different group, as you can probably verify by omitting some of the relations in the two presentations we gave for $D_3$. Indeed, we can very easily obtain various infinite groups by omitting relations. In particular, if we omit all the relations in our two presentations, we obtain the free group on two generators, an infinite nonabelian group.)

But in any case, you can (I hope) now understand rather vividly a key definition: the diameter of the Cayley digraph is the longest length of any minimal length word. In the simple example we have been discussing, you can easily see that we can get from e to any element in just two moves, so the diameter is two.

Now we come to another essential point: each group has many possible generating sets, and different ones will almost always result in Cayley digraphs which are non-isomorphic, and which indeed have different diameters.

For example, you can also generate the permutation group we are using the represent the dihedral group on six elements (the symmetry group of an equilateral triangle) by using three transpositions (a transposition is a permutation of two elements) $(1,2), \; (2,3), \; (3,1)$:

gap> FF := FreeGroup("a","b");
<free group on the generators [ a, b ]>
gap> GG := FF/[ FF.1^2, FF.2^2, (FF.1*FF.2)^3 ];
<fp group on the generators [ a, b ]>
gap> Size(GG);
6
gap> IsomorphismGroups(GG, DihedralGroup(6));
[ a, b ] -> [ f1, f1*f2 ]
gap> IsomorphismGroups(GG,G);
[ a, b ] -> [ f, f*r ]

The last gives an explicit isomorphism
$$a \rightarrow f, \; b \rightarrow fr$$
Or, loosely speaking
$$a = f = (2,3), \; b = f \,r = (2,3) \; (1,2,3) = (1,2)$$
This leads to a very different looking Cayley digraph; see the rightmost graphs in the first and second figures.

Figures (left to right):

• Two Presentations of $D_3$
  • Left: $\left< \, r, \, f \, | \, r^3 = f^2 = (f \, r)^2 = e \, \right>$
  • RIght: $\left< \, a, \, b \, | \, a^2 = b^2 = (ab)^3 = e \right>$
  Here, the two Cayley digraphs are drawn unlabeled, to emphasize that they are homogeneous; all vertices are equivalent.
• The same two presentations, with one vertex arbitrarily labeled e, which then leads to labels for all the other vertices by following arrows in the graph. Note that this labeling completely breaks the symmetry of the Cayley digraphs!
• A graphical illustration of the multiplication of two permutations left to right.

 

[Chris Hillman]

BRS: Exploring the Rubik Group with GAP. III. Cayley Digraphs (cont'd)

(continued)

Notice that, starting from e, it takes three moves in the new generators to reach one of the five other elements, so the diameter of the new Cayley digraph (for the very same group!) is three. See the first figure below.

As an exercise, try adding the correct labels of the vertices in our two Cayley digraphs using permutations written in the "product of disjoint cycles notation" which we have been using (see any group theory book if it isn't clear), and verifying that everything is consistent: left to right multiplication by following arrows in the Cayley digraphs agrees with the usual rules for multiplying permutations. See the second figure below, and notice for example that consistency requires that $(1,3) \, (2,3) = (1,2,3)$, which is true.

Notice that unlike labeling the vertices with one of infinitely many equivalent words in a given generating set, the labels in terms of the standard notation for permutations are unique. Both ways of labeling are very useful in their way!

By the way, if you know about reflection groups and/or the Weyl group associated with a semisimple Lie algebra, you may recognize the second presentation as a simple example of a Weyl group!

I cannot resist adding a table suggesting some more interesting ways in which $D_3$ arises naturally in various areas of mathematics:
$$\begin{array}{llll} \hbox{pres.} & \hbox{perm.} & GL(2,2) & \hbox{Moebius} \\ \hline \\ e & () & \left( \begin{array}{cc} 1&0\\0&1\end{array} \right) & z \rightarrow z \\&&&\\ r & (1,2,3) & \left( \begin{array}{cc} 1&1\\1&0\end{array} \right) & z \rightarrow (z-1)/z \\&&&\\ r^2 & (1,3,2) & \left( \begin{array}{cc} 0&1\\1&1\end{array} \right) & z \rightarrow 1/(1-z) \\&&&\\ b=f & (1,2) & \left( \begin{array}{cc} 1&0\\1&1\end{array} \right) & z \rightarrow z/(z-1) \\&&&\\ && \left( \begin{array}{cc} 1&1\\0&1\end{array} \right) & z \rightarrow 1-z \\&&&\\ && \left( \begin{array}{cc} 0&1\\1&0\end{array} \right) & z \rightarrow 1/z \end{array}$$
Here, the third column enumerates the elements of a subgroup of $GL(2,2)$ which is isomorphic to $D_3$, where the group multiplication is matrix multiplication, and the fourth column enumerates the corresponding elements of a subgroup of the Moebius group which is isomorphic to $D_3$, where the group multiplication is composition of transformations. Some of you may recall that the Moebius group is isomorphic to the Lorentz group! I left a few entries blank so you can fill them in yourself.

Here, $GL(2,2)$ is the group of 2x2 matrices with entries in the finite field with two elements, so the third column gives an example of a linear representation of an abstractly defined group, while the fourth column gives a representation of the same group as a nonlinear transformation group. If you want to play with this, here is how to define the matrix group in GAP:

gap> z := Z(2);
Z(2)^0
gap> m1 := [[z^0,z^0], [z^0, 0*z]];
[ [ Z(2)^0, Z(2)^0 ], [ Z(2)^0, 0*Z(2) ] ]
gap> Display(m1); 
 1 1
 1 .
gap> m2 := [[z^0, 0*z],[ z^0, z^0 ]];
[ [ Z(2)^0, 0*Z(2) ], [ Z(2)^0, Z(2)^0 ] ]
gap> Display(m2);
 1 .
 1 1
gap> Order(m1); Order(m2);
3
2
gap> P := Group(m1,m2);
Group([ <an immutable 2x2 matrix over GF2>,
  <an immutable 2x2 matrix over GF2> ])
gap> Order(P);
6
IsomorphismGroups(G,P);
[ r, f ] -> [ <an immutable 2x2 matrix over GF2>,
  <an immutable 2x2 matrix over GF2> ]

Here, we told GAP to define a symbol for a generator of the finite field GF(2), then we defined two 2x2 matrices over that field using GAP's rather quirky but unambiguous notation for finite fields, we verified that they have the expected orders, we computed the group generated by those two matrices, and finally we computed an isomorphism with a group we already know is GAP's "official definition" of the dihedral group $D_3$.

A maddening notational conflict: it is traditional to write composition of transformations from right to left $(f_2 \circ f_1)(x) = f_2(f_2(x))$, which means [itex] x \rightarrow f_1(x) \rightarrow (f_2 \circ f_1)(x)[/tex]. This would correspond to using left actions, whereas we are in effect writing composition left to right, i.e. using right actions, which we need to do in order to make following arrows in our Cayley digraphs consist with our multiplication of permutations. This is probably confusing if you are not already used to it, so I suggest simply ignoring the issue until you absolutely must confront it.

Figures (left to right):

• the same Cayley digraphs, with vertices labeled with distances from e (the red vertex),
• the same Cayley digraphs, with vertices labeled by permutations,
• the equilateral triangle with vertices as labeled by GAP session; the three reflections (elements of order two) are shown; the generator $r$ corresponds to a clockwise 1/3 turn about the centroid, taking $1 \rightarrow 2 \rightarrow 3$.

 

[Chris Hillman]

RS: Exploring the Rubik Group with GAP. III. Cayley Digraphs (cont'd)

To drive home the point, I should really draw a few more Cayley digraphs associated with presentations of familiar finite groups. I'm too lazy to draw very many, so I'll just draw some for presentations of the symmetric group on four letters $S_4$.

One generating set which is often encountered as one generator of order four, $a$, and another of order two, $b$; following the convention mentioned above, the corresponding pairs of directed edges $b^{\pm 1}$ are drawn as a single undirected edge to avoid needless clutter. The presentation gives relations obeyed by these generators sufficient to uniquely define the group we mean. It is
$$\left< a, \, b | a^4 = b^2 =(ab)^3 = e \right>$$
where as always $e$ stands for the identity element. See the figure below and verify that, for example, starting from any vertex, following the word $ababab = (ab)^3$ leads back to the starting vertex, which verifies the relation $(ab)^3 = e$.

How do I know that the given relations define the intended group and not some other? Well, I have studied some combinatorial group theory. But the "cheap answer" is that you don't really need to know much about combinatorial group theory to verify that this is a legal presentation of $S_4$ using GAP. Here are the commands you need:

gap> F := FreeGroup(2);
<free group on the generators [ f1, f2 ]>
gap> a := F.1;; b := F.2;;
gap> G := F/[ a^4, b^2, (a*b)^3 ];
<fp group on the generators [ f1, f2 ]>
gap> Size(G);
24
gap> IsomorphismGroups(G,SymmetricGroup(4));
[ f1, f2 ] -> [ (1,4,3,2), (1,4) ]

For further practice, try to verify that the diameter of this Cayley digraph is six (that is, starting from any vertex v1, there is a vertex v2 such that you must transverse six edges to get from v1 to v2, but six edges suffice to reach any vertex) and the girth is 4 (because the "squares" require four edges to transverse in a loop).

Cayley himself used distinct colors to denote the directed edges corresponding to distinct generators. For example, a presentation using three elements of order two is
$$\left< a, \, b, \, c | a^2 = b^2 = c^2 = (ab)^3 = (bc)^3 = (ac)^2 \right>$$
Once again, we can verify that this really is a presentation of $S_4$ using GAP:

gap> F := FreeGroup(3);
<free group on the generators [ f1, f2, f3 ]>
gap> a := F.1;; b := F.2;; c := F.3;;
gap> G := F/[ a^2, b^2, c^2, (a*b)^3, (a*c)^3, (b*c)^2 ];
<fp group on the generators [ f1, f2, f3 ]>
gap> Size(G);
24
gap> IsomorphismGroups(G,SymmetricGroup(4));
[ f1, f2, f3 ] -> [ (2,3), (3,4), (1,2) ]

See the figure below and verify the relations. Also verify that the diameter of this Cayley digraph is again 6, but this time the girth is 3. You can also label the vertices with words in the generators; choose any vertex to label $e$ and then follow edges to label the other vertices with some word. Then, using the isomorphism provided by GAP, you can also label each vertex with precisely one of the 24 permutations in $S_4$; the trivial permutation $()$ is the new label of the vertex previously labeled by $e$.

If know about Schlegel diagrams for polytopes, you might recognize that these Cayley digraphs are secretly based upon the Schlegel diagram for a truncated octahedron. There are actually six "squares" in these diagrams, not five!

Notice that the letters in the presentations mostly play the role of "dummy variables", so I reused the same letters in the second presentation. To avoid possible confusion I could have used three new letters instead.

Exercise: another presentation of $S_4$ uses one generator of order three and one of order two:
$$\left< \, r, \, f \, | \, r^3 = f^2 = (rf)^4 = e \, \right>$$
Verify using GAP that this really does yield $S_4$ and find an explicit isomorphism. Verify that the new Cayley digraph has diameter 6 and girth 3. (Hint: Schlegel diagram for a truncated cube; the new Cayley digraph will have 8 "triangles" instead of six "squares".)

Exercise: use GAP to verify that one presentation of the alternating group on four letters $A_4$ is
$$\left< \, s, \, t \, | \, s^3 = t^2 = (st)^3 = e \, \right>$$
Draw the Cayley digraph (truncated tetrahedron!). What is its diameter and girth?

If you have read this far, you have probably noticed that all our Cayley digraphs have a very strong and striking property: they are homogeneous in the sense that all vertices are equivalent. This is true for all Cayley digraphs.

But by no means are all paths in a typical Cayley digraph equivalent: they cannot be, because elements of groups can typically have many different orders, and can differ from each other in more subtle ways, and it is words in the generators used in the given presentation, i.e. paths in our digraph, which represent the group elements.

It is quite possible to obtain finitely presented but (countably) infinite groups. For example,
$$\left< \, s, \, t \, | \, s^3 = t^2 = e \, \right>$$
does not give any relationship at all between s,t. In particular, they do not commute. So this is the "free product" of the cyclic groups $C_2, \, C_3$; there is a picture of (a local neighborhood of) its Cayley digraph in the textbook by Hatcher, Algebraic Topology.

Figures (left to right):

• Cayley digraph for the presentation of $S_4$ given by
  $$\left< \, a, \, b \, | \, a^4 = b^2 = (ab)^3 = e \, \right>$$
• Cayley digraph for the presentation of $S_4$ given by
  $$\left< \, a, \, b, \, c \, | \, a^2 = b^2 = c^2 = (ab)^3 = (bc)^3 = (ac)^2 = e \, \right>$$

 

[Chris Hillman]

BRS: Exploring the Rubik Group with GAP. IV. G-Sets and Schreier Digraphs

Now we come to one of my favorite things: group actions, the category of G-sets (where G is some group), and their Schreier digraphs (in the case when G is finitely presented). I'd like to try to explain these notions using pictures rather than formal definitions, so:

Consider again the Cayley digraph for the presentation
$$\left< a, \, b, \, c, | \, a^2 = b^2 = c^2 = (ab)^3 = (bc)^3 = (ab)^2 \right>$$
which as you recall turns out to present the symmetric group on four letters, S_4. Now, what do you think the digraph in the figure below means?

Sure, it is the Schreier digraph defining (up to S_4-isomorphism) a particular example of an S_4-set, but what do you guess that this digraph says?

You probably guessed: we have a set containing $3+6+8+2+2=21$ elements, with something called "a group action by S_4", which is defined by saying how each generator in the presentation moves each element, which is expressed graphically by following the appropriate colored directed edge.

Which is of course the correct answer. And of course there must be some restriction on how the generators can act to define an action. What do you think that condition might be, from the picture?

You probably guessed: we must be able to follow the directed edges in sequence, while ensuring that following a word like $(ab)^3$ gives the same result as the alternative word $e$, and similarly for any pair of equivalent words.

Which is of course the correct answer.

Here is a formal definition: a group G is said to act (from the right) on a set X if for any x in X,

• $x.e = x$,
• for any $g_1, \, g_2$ in G, we must have
  $$(x.g_1).g_2 = x.(g_1 \, g_2)$$

Here, the action is denoted by a dot, x.g, and group multiplication by concatenation. These are the minimal requirements which ensure that our Schreier digraphs are self-consistent. Usually one only uses Schreier digraphs to define actions by a finitely-presented group G, for a particular presentation, but the formal definition works for any G and any X, independent of any presentation of G.

Exercise: redraw the Schreier digraph of our example using the first presentation of S_4 which I introduced above.

You no doubt noticed that our example S_4-set consists of five subsets such that the action never moves an element in one of these five subsets outside the subset. Such subsets are called orbits. In general, a G-set with only one orbit is said to be transitive. In the theory of G-sets, one operation of fundamental importance is the sum (or coproduct) $X \amalg Y$ of two G-sets $X, \, Y$. Its easy to say how to form the sum of two finite G-sets (G-finitely presented) in terms of their Schreier diagrams: simply draw the two diagrams side by side and declare the result to be one diagram. In particular, any G-set is the sum of its orbits.

You probably noticed that unlike Cayley digraphs, Schreier digraphs are in general not homogeneous. Indeed, they are homogeneous exactly in the special case of a G-set which happens to be a group in its own right (it turns out that in this case it must be quotient group of G).

In the orbit depicted at upper right in our example Schreier digraph, the leftmost point is fixed by two of the given generators but moved by the third. We say that its stabilizer subgroup is $H = \left< a, \, c \right>$. In general, given a subset A of X, its pointwise stabilizer (a better term might be "fixgroup") is
$$A \rhd = \left\{ g \in G : x.g = x, \; \forall x \in A \right\}$$
There is a dual notion: the fixset of a subgroup H of G is
$$\lhd H = \left\{ x \in X : x.g = x, \; \forall g \in H \right\}$$
The setwise stabilizer (a better term might be isotropy subgroup) is a bit different from the point stabilizer:
$$G_A = \left\{ g \in G : A.g \subset A, \; \forall x \in A \right\}$$
The distinction is that the fixgroup of A consists of all group elements which fix every point in A, whereas the isotropy group of A consists of all group elements which move A to itself (in the case of finite X, or into itself in the case of infinite X). (This distinction is obviously immaterial when A consists of a single element of X!) It turns out that fixgroups have much nicer formal properties than isotropy groups, which is crucial for classical Galois theory (which we can think of as concerning certain actions on roots of polynomials in one variable, with coefficients in various fields).

Exercise: in our example, what is the fixset of a? (I.e., the subgroup generated by a, $\left\{ e, \, a \right\}$.) How about b and c? And b,c together?

Figures:

• An example of an S_4-set, defined by exhibiting its Schreier digraph.

 

[Chris Hillman]

RS: Exploring the Rubik Group with GAP. IV. G-Sets and Schreier Digraphs (cont'd)

(continued...)

For any G, G-sets form a category, which means there is a notion of G-homomorphisms and G-isomorphisms. You probably immediately guess that however these notions are defined, they must ensure that the Schreier graphs of isomorphic G-sets are the same (except for relabeling the points), assuming you are using the same presentation of G for each of the Schreier diagrams. Which is of course correct. For example, two of the orbits in our diagram depict isomorphic (transitive) sub-G-sets, but the other three are all distinct as (transitive) sub-G-sets from these.

If you are really on the ball, you might be able to guess that G-homs must have the property that to define a G-hom from X to Y, it must suffice to define the image of one point in each orbit of X.

A G-congruence is an equivalence relation on a G-set X such that $x_1.g \sim x_2.g$ whenever $x_1 \sim x_2$. The equivalence classes of a G-congruence form the quotient $X/\sim$. This notion is equivalent to the notion of a G-epimorphic image of X.

Mathematicians study (and physicists use) many different categories, such as the categories of

• groups,
• rings,
• fields,
• vectors spaces over F, F a field,
• R-modules, R a group,
• linear associative algebras over F,
• real (or complex) Lie algebras,
• real Lie groups,
• smooth manifolds
• graphs
• ...

But only rarely can we obtain general structure theorems describing how to build an arbitrary object in the category from "simple" objects. And for only a tiny handful can we explicitly describe the automorphism group of each object. The category of G-sets, like the category of finite-dimensional real vector spaces, is such an exceptionally nice category!

You have probably guessed that not only is a G-set is "a set with added structure" (defined by the group structure of G), but a G-homomorphism is a mapping from one set to another which preserves this extra structure. From this coy admission you can probably figure out what the formal definition must be!

In category theory, we either come to grief, or learn not to expect that in a category new to our experience, a monomorphism is a one-one homomorphism, or that an epimorphism is an onto homomorphism. (The last fails in the category of groups, for example.) But in the category of G-sets these desirable properties are true!

I already pointed out that every G-set is the coproduct of its own orbits, which already tells us that it suffices to obtain structure theorems for transitive G-sets. Here they are (for those of you how already know about conjugate subgroups and the cosets of a subgroup):

• Every transitive G-set, X, is G-isomorphic to the set of right cosets $H \!\setminus\! G$, where H is the fixgroup of any element of X, and where the action on the right coset $H \, g_0$ by $g \in G$ is $(Hg_0).g \rightarrow H \, (g_0.g)$
• For any subgroups H, K of G, there is a G-epimorphism from H\G to K\G precisely in case H lies in some conjugate of K. In particular, the conjugacy classes of subgroups of G are in bijection with the transitive G-sets, up to G-isomorphism.
• If X is a transitive G-set--- without loss of generality suppose it is H\G--- then the group of G-automorphisms of X is $H \!\setminus\! N_G(H)$, where $N_G(H)$ is the normalizer of H in G (the largest subgroup of G in which H is normal).

If X is a G-set and K is a subgroup of G, then X is also an K-set under the action obtained by simply restricting the original action to elements of H. In the case of a transitive G-set, say H\G, usually the restriction to K means that the coset space breaks up into several orbits under K. There is an explicit formula saying precisely how this happens, which involves the so-called double cosets $H \!\setminus\! G / K$.

These structure theorems imply that if we know the lattice of subgroups of G taken up to conjugacy, $H \rightarrow g^{-1} H g$, we know the classification of transitive G-sets up to G-isomorphism, and all G-sets are simply sums (possibly with repeated summands) of these. So if we can draw Schreier diagrams for the coset space $H \!\setminus\! G$, for each conjugacy class of a subgroup of G, we can draw the Schreier diagram of any G-set.

GAP can help you do all these things! The most useful way to obtain the subgroup lattice of a reasonably small finite group obtained via a given presentation is:

gap> F := FreeGroup(3);
<free group on the generators [ f1, f2, f3 ]>
gap> a := F.1; b := F.2; c := F.3;
f1
f2
f3
gap> G := F/[ a^2, b^2, c^2, (a*b)^3, (a*c)^3, (b*c)^2 ];
<fp group on the generators [ f1, f2, f3 ]>
gap> tom := TableOfMarks(G);
TableOfMarks( <fp group of size 24 on the generators [ f1, f2, f3 ]> )
gap> Display(tom, rec( form := "supergroups"));
 1:  1
 2:  3 1
 3:  6 . 1
 4:  4 . . 1
 5:  1 1 . . 1
 6:  3 1 1 . . 1
 7:  3 1 . . . . 1
 8:  4 . 2 1 . . . 1
 9:  3 3 1 . 3 1 1 . 1
10:  1 1 . 1 1 . . . . 1
11:  1 1 1 1 1 1 1 1 1 1 1

gap> Display(tom, rec( form := "subgroups"));
 1:  1
 2:  1 1
 3:  1 . 1
 4:  1 . . 1
 5:  1 3 . . 1
 6:  1 1 2 . . 1
 7:  1 1 . . . . 1
 8:  1 . 3 1 . . . 1
 9:  1 3 2 . 1 1 1 . 1
10:  1 3 . 4 1 . . . . 1
11:  1 3 6 4 1 3 3 4 3 1 1

gap> OrdersTom(tom);
[ 1, 2, 2, 3, 4, 4, 4, 6, 8, 12, 24 ]
gap>  List([1..11], j-> [j,IdSmallGroup(RepresentativeTom(tom,j))]);
[ [ 1, [ 1, 1 ] ], [ 2, [ 2, 1 ] ], [ 3, [ 2, 1 ] ], [ 4, [ 3, 1 ] ],
  [ 5, [ 4, 2 ] ], [ 6, [ 4, 2 ] ], [ 7, [ 4, 1 ] ], [ 8, [ 6, 1 ] ],
  [ 9, [ 8, 3 ] ], [ 10, [ 12, 3 ] ], [ 11, [ 24, 12 ] ] ]

Exercise: see if you can figure out from the extensive GAP documentation and from the discussion so far how to use the GAP output quoted above to construct the lattice of subgroups of S_4 up to conjugacy. See my Post #1 in the BRS Thread on "Subgroup Lattice of a Permutation Group via GAP"

www.physicsforums.com/showthread.php?t=385803

See in particular the "key to SmallGroup" in that post and the figure, which shows the subgroup lattice up to conjugacy. In the figure--- unfortunately, VB won't permit to attach a copy as a figure at the end of this post!--- the "fraction" p/q decorating the edge from the class of H to the class of a smaller subgroup K means that each subgroup in the upper class includes p subgroups from the lower class, and each subgroup in the lower class is included in q subgroups in the upper class. This information is read off the "table of marks" in the GAP output I quoted.

Then, to construct a permutation representation of the coset space of, say, class 8 (which consists of four subgroups each isomorphic to SmallGroup(6,1) or S_3):

Action(G, RightCosets(G,RepresentativeTom(tom,8)), OnRight);
Group([ (2,3), (1,2), (3,4) ])
gap> NrMovedPoints(last);
4

Exercise: figure out how to draw the Schreier digraph, with respect to the chosen presentation of S_4, for this coset space, from the GAP output just quoted. (Hint: the coset space contains four cosets, numbered 1..4, and the generator a of S_4 in our chosen presentation acts like the transposition (2,3). Similarly for b,c.)

Excercise: draw Schreier digraphs for each transitive S4-set, using the procedure just sketched. Figure out which conjugacy class corresponds to which orbit in the example of a five orbit S_4-set which I gave earlier. Compare the digraphs for the maximal and the normal subgroups with the others.

G itself is a G-set under the action $g_0 \, g \rightarrow g$. Sums of copies of G under this action form "free" G-sets, also called torsors. In general, the category of G-sets has poor lifting properties (torsors are the only projective G-sets) but excellent extension properties (every G-set is injective). Every G-set is the quotient (equivalently, the G-epimorphic image of) some torsor.

Primitive G-sets are a particularly important type of transitive G-set: they are the ones which have no nontrivial quotients, i.e. which are not the G-epimorphic images of other G-sets. By our structure theorem, they are all given up to G-isomorphism by the coset spaces M\G where M is a maximal subgroup of G. Then, it turns out that using the notion of skew products, we can build up any transitive G-set by taking suitable iterated skew products of primitive G-sets. And then, as already remarked, by taking a coproduct we can obtain an arbitrary G-set. So the primitive G-sets are of great importance in the theory.

If you know anything about the category of R-modules, R a ring, you probably already noticed that the theory of G-sets appears to have many similarities. In particular, primitive G-sets are clearly analogous to irreducible R-modules.

Furthermore, the normal subgroups of G are precisely those whose conjugacy class consists of just one subgroup N, and this happens exactly in case the coset space N\G is in fact a group in its own right. By the fundamental theorem of groups, this group is a factor group of G, an epimorphic image under a group homomorphism whose kernel is N itself. Intuitively, a Cayley digraph for factor group (wrt some presentation) should reveal how N\G is a "simplified model" for G in which some structure has been "idealized away", namely all and only the structure contained in the subgroup N.

In the same spirit, a Schreier digraph for a quotient G-set $Y = X/~\sim$ of a G-set X (equivalently, a G-epimorphic image of X) should reveal how Y is a simplified model of X in which certain structure has been "idealized away".

There are three important and useful notions of the "product" of two G-sets: the direct product, the wreath product, and the skew product (with respect to a given cocycle). The direct product has an obvious definition; the other two might appear forbidding if I wrote down formal definitions, so I'll be coy again. Here I'll just say that the general idea of the wreath product is to take copies of X--- as many copies as there are elements of Y--- and to act within each copy of X in the obvious way, and to swap the copies like the action on Y. Then since it should appear plausible that G-automorphisms of an arbitrary G-set Z can arbitrarily permute G-isomorphic orbits of Z, and since we know the automorphism group of each orbit, it should be plausible that using wreath products we can write a formula for the automorphism group of a general G-set.

If X, Y are two G-sets, then Y^X, the set of all G-homormorphisms from X to Y, is also a G-set in a way which is defined in the spirit of category theory via a universal mapping property. Coproducts, direct products, and some other important notions can also be defined by UMPs. In fact, one of the nice (and rare) properties of the category of G-sets is that it is an elementary topos, which in simple terms means that the notion of a G-set is so powerful, in terms of mathematical logic, that we could found all of mathematics upon this notion, instead of upon the notion of a "naked set". To be sure, I am not aware of any interesting consequences of this rather startling assertion!

You've probably noticed that I've been rather cavalier about whether I am talking about finite G-sets, countable ones, or arbitrarily large ones. This defect is remediable. I should also stress that the theory of finite G-sets is very closely related to the theory of permutation representations of finite groups, if not quite the same thing, exactly. One of the major thrusts of the theory of permutation representations is the surprising and deep fact that multiple transitivity is rare. But I won't explain why or even what that means, even though it is relevant to stuff I do plan to discuss.

 

[Chris Hillman]

Exploring the Rubik Group with GAP. IV. G-Sets and Schreier Digraphs (cont'd)

(continued)

I should say just a bit about the Galois theory of G-sets, by which I mean the (quite easy!) theory associated with fixgroups and fixsets. The key observation is the fact that if A, B are any two subsets of X, then
$$(A \cup B) \rhd = A \rhd \cap B \rhd$$
Nothing like this is true for setwise stabilizers!

It turns out that the fixgroups $A \rhd$ form a complete sublattice of the lattice of subgroups of G, and the fixsets $\lhd H$ form a complete sublattice of of the lattice of subsets of X, and these sublattices are dual in the order reversing sense of Galois theory. (So, smaller fixgroups correspond to bigger fixsets).

The fixset of the fixgroup of the subset A swallows A, $A \subset \lhd A \rhd$, and this operation gives what is called a closure operator, which generalizes, among other things, the notions of:

• the span of a subset of a finite dimensional vector space,
• the subgroup generated by a subset of elements of the group,
• topological closure

All the fixsets in the lattice of fixsets arise in this way. Furthermore, G acts on its subgroups by conjugation, and
$$(A.g) \rhd = g^{-1} \, A \rhd \, g$$
So our dual lattices are invariant under the appropriate actions by G. In fact, it's usually best to think of them as one lattice whose elements are pairs $(A,H)$ where A is a fixset and H is a fixgroup. Then the action is
$$(A,H).g = (A.g, g^{-1} H g)$$

What is the significance of the closure $\lhd A \rhd$ of the subset A? It is the smallest fixset which swallows A, but we can say more: it is precisely the set of elements of X whose motions under the action are all completely determined by the motions of A. That is, via the action by G on X, each group element g defines an invertible transformation of X, which takes each x in A to some target. Often information about the effect of g on A implies something about the effect of g on some additional elements of X. The largest set whose motions are determined in this sense by the motions of A is the closure of A, $\lhd A \rhd$.

By this point you have probably guessed that the transitive G-sets of form $A \rhd \!\setminus\! G$, or $A \cdot G$ are important. Indeed they are. They are called complexions.

One reason why the formula $(A \cup B) \rhd = A \rhd \cap B \rhd$ is so important is that the conditional complexions $A \cdot (B \rhd)$ obey a "quotient law": the joint complexion
$$(A \cup B) \cdot G \simeq (A \cup B) \rhd \!\setminus\! G \simeq \left( A \rhd \cap B \rhd \right) \!\setminus\! G$$
is a skew product of the conditional complexion $B \cdot A \rhd$ with the complexion $A \cdot G$, and also of $A \cdot B \rhd$ with $B \cdot G$. Because for any two subgroups H,K of a finite group G we have,
$$| (H \cap K) \!\setminus\! G | = | (H \cap K) \!\setminus\! H | \cdot | H \!\setminus\! G |$$
we immediately conclude that
$$\log | (H \cap K) \!\setminus\! G | = \log | (H \cap K) \!\setminus\! H | + \log | H \!\setminus\! G |$$
This means that in the case of a finite group G, the log of the size of the complexion, $H(A) = \log | A \cdot G |$, and similarly $H(A \!\setminus\! B) = \log | A \cdot B\rhd |$ yields kinematical notions of entropy and conditional entropy (respectively) which satisfy the same nice formal properties as Shannon's entropies, and which generalizes Boltzmann's notion of the entropy associated with "microstates" and "macrostates".

A Boltzmann entropy is the log of a multinomial coefficient; a classic approximation due to Stirling shows that when all the $n_j$ are large,
$$\log \left( \begin{array}{ccccc} &&n&& \\ n_1 & n_2 & \ldots & n_{r-1} & n_r \end{array} \right) \approx -\sum \frac{n_j}{n} \log \frac{n_j}{n}$$
which has the form of Shannon's entropy. By formal properties of entropies, I mean things like

• $0 \leq H(B \!\setminus\! A) \leq H(A)$, with equality having a particular significance,
• $H(A \cup B) \leq H(A) +H(B)$, with equality having a particular significance,
• $H(A \!\setminus B) = H(A \cup B) - H(B)$
• the quotient law: $H(A \cup B) = H(A \!\setminus\! B) + H(B) = H(B \!\setminus\! A) + H(A)$
• Rokhlin distance $d(A,B) = H(A \!\setminus \! B)+H(B \!\setminus\! A)$ obeys triangle inequality and all that,
• ...

(I'll give anyone interested a chance to try to figure out how these kinematical entropies generalize Boltzmann entropies before I say more. Here's a hint: from an action by G on X we obtain an induced action on partitions of X, which has some particularly nice properties.)

And when G is a finite dimensional Lie group, the dimension of the complexions serve as kinematical entropies.

In this informational-theoretic approach, the complexion $A \cdot G$ is precisely what we need to describe the pointwise motions of A under the given right action by G on X. It turns out that, as must happen, $\lhd\! A \!\rhd \cdot G$ is G-isomorphic to $A \cdot G$. Furthermore, $A \cdot B\!\rhd$ describes the pointwise motions of A under the fixgroup of B, and is in bijective correspondence with $A \cdot B\!\rhd g$ for some coset $B\!\rhd g \in B\!\rhd \!\setminus G$. Thus:

• $H(A)$ measures the variety of ways in which we can move A, and thus measures the information required to describe the motions of A under an arbitrary element of G. It also measures the "asymmetry" of A under G (thought of as a symmetry group, a group of transformations on X).
• $H(A \!\setminus B) = H(A \cup B) - H(B)$ measures the variety of ways in which we can move A while pointwise fixing B, or while moving B by an unknown element $g \in G$ (possibly not in the fixgroup of B), and thus measures the information required to describe the possible motions of A under an unknown element $g \in G$, given knowledge of the motions of B under g.
• The expression
  $$I(A,B) = H(A) +H(B) - H(A \cup B) = H(A) - H(B \!\setminus\! A) = H(B) - H(A \!\setminus\! B)$$
  measures the information we gain about the motion of A under an unknown element $g \in G$ if we learn the motion of B under g, and vice versa.

This discussion has been quite abstract! The picture I am trying to convey will become much more vivid, I think, once I have a chance to discuss some explicit examples. If you can't wait, a particularly good example to work out is the case of the action of the projective linear group on points of a projective space. Even better, if you can figure out what happens when you restrict this action to the affine group. Even better, if you can throw in the action on lines, 2-flats, and so forth. And you can compare projective spaces over finite fields with real projective space. Then there are euclidean spaces, symplectic spaces...

I hinted at one reason why skew products are important, but I haven't said anything yet about how to define them. One reason why not is that this notion requires saying something about a kind of cohomology, because we need a notion of a certain kind of cocycle which is a special map of form $H \leftarrow X \times G$. Let me avoid that by recounting an anecdote.

The first textbook in English on group theory was published by Burnside in 1911. One important topic covered was a notion introduced by Frobenius, the so called table of marks of G, which tabulates a host of information such as the number of conjugates of a subgroup H which sit inside K. From what I said above you can probably see that this kind of information is very useful for studying G-sets! And thus, for permutation representations of G.

In the forward to the first edition of his textbook, Burnside remarked that he had not included the remarkable (and then very new) theory of linear representations which had been introduced by Frobenius subsequent to his work on permutation representations, because this theory had not yet resulted in theorems which could not be proven by other means. In the second edition, Burnside, who had since used linear representations to prove a now famous theorem which neither he nor anyone else had been able to prove by other means, was happy to include a new chapter on linear representations--- at the expense of removing from the chapter on permutation representations the material on the "table of marks"! This choice seems to have had the unfortunate effect that several generations of mathematicians have never encountered the notion of the table of marks. Even worse, have never encountered the notion of a Frobenius cocycle.

And what is a Frobenius cocycle? Well, its an easy way to obtain a cocycle from a right transvesal for a given coset space H\G which is suitable for constructing a skew product of H\G and H. More generally, it allows you, given the Schreier diagrams of the coset sets $G_{j+1} \!\setminus\! G_j$ which appear in a (possibly non-subnormal) series of subgroups
$$1 < G_r < \ldots < G_2 < G_1 < G$$
to construct the Schreier diagrams of iterated skew products built from the $G_{j+1} \!\setminus\! G_j$. In particular, to construct the Cayley graph of G itself. And Frobenius knew this! Although, because the notion of cohomology didn't appear until later in the 20th century, he did not use the term "cocycle".

 

[Chris Hillman]

Exploring the Rubik Group with GAP. V. The Rubik Group

But wait a minute!, you protest. Didn't I say that an open problem for thirty years has been to compute the diameter of the Cayley digraph of the Rubik group? Well, yes. But just because Frobenius could have told you over a century ago how to construct the Cayley digraph of the Rubik group (because, as we'll see, you can construct and even draw on not terribly oversized sheets of paper the Schreier digraphs we need using GAP), this doesn't mean that computing the diameter of this digraph is easy.

But I am of course getting ahead of the story. It is high time that I say exactly what is this Rubik group to which I keep referring.