- #1
- 2,355
- 10
For another BRS thread, I looked up some information at http://www.genealogy.ams.org/ and was completely sidetracked by my attempt to look up the genealogies of my undergraduate mentors 
Seriously, physics needs a tool like this, because it really does give amazing insight into the natural line of development seen in mathematics when you know enough to pick out the threads.
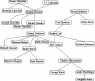
The graph of "geneological descent" rapidly becomes utterly unwieldy, but I'll try to keep a few partial graphs in this thread, with some explanatory glosses. The full graph is not a tree in the sense of graph theory, because some people have two supervisors, which rapidly tangles up doctorvater relationships into a complicated network.
It is interesting to see that certain persons function as highly connected nodes in the graph. Some of the best known names turn out to have thousands of descendants--- Carl Friedrich Gauss, for example, has almost 50,000 mathematical descendents. Other lines die out immediately for sad reasons, e.g. Niels Abel (died too young to have any students). A handful of persons, such as George Green, who are now regarded as great mathematicians don't appear at all because they were amateurs who never earned a formal Ph.D. And if you go back far enough, the academic system as we know it (in which a professor has doctoral students) simply had not developed. And some differences between different systems, e.g. "imperial" Germany, France, the UK, the Soviet Union, and the U.S. become apparent.
It's also interesting to see that leading mathematicians are often biologically related--- it's no accident that as you trawl through these trees you will see certain family names multiple times. Mathematical marraiges can reveal natural lines of development in the history of mathematics. Just to add to the fun, some of the people who appear are also biologically related to certain persons whom I would have to characterize as... dissidents.
If you know about youthful friendships and who was a post-doc of whom, you can learn even more. E.g. Emmy Noether was a post-doc of David Hilbert in Goettingen, where other great mathematicians on the faculty included Felix Klein and Hermann Minkowski. And Klein and Lie were student friends who greatly influenced each other. Eventually I hope to tie this all into explaining how "Noether's theorem" as known to physicists is a pale shadow of the actual result, which belongs to Klein's theory of symmetries of differential equations (the ones generated by a Lagrangian).
Seriously, this is a rich resource for anyone interested in the history of physics (because so many mathematicians played a crucial role in physics via their mathematical insights).
Seriously, physics needs a tool like this, because it really does give amazing insight into the natural line of development seen in mathematics when you know enough to pick out the threads.
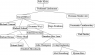
The graph of "geneological descent" rapidly becomes utterly unwieldy, but I'll try to keep a few partial graphs in this thread, with some explanatory glosses. The full graph is not a tree in the sense of graph theory, because some people have two supervisors, which rapidly tangles up doctorvater relationships into a complicated network.
It is interesting to see that certain persons function as highly connected nodes in the graph. Some of the best known names turn out to have thousands of descendants--- Carl Friedrich Gauss, for example, has almost 50,000 mathematical descendents. Other lines die out immediately for sad reasons, e.g. Niels Abel (died too young to have any students). A handful of persons, such as George Green, who are now regarded as great mathematicians don't appear at all because they were amateurs who never earned a formal Ph.D. And if you go back far enough, the academic system as we know it (in which a professor has doctoral students) simply had not developed. And some differences between different systems, e.g. "imperial" Germany, France, the UK, the Soviet Union, and the U.S. become apparent.
It's also interesting to see that leading mathematicians are often biologically related--- it's no accident that as you trawl through these trees you will see certain family names multiple times. Mathematical marraiges can reveal natural lines of development in the history of mathematics. Just to add to the fun, some of the people who appear are also biologically related to certain persons whom I would have to characterize as... dissidents.
If you know about youthful friendships and who was a post-doc of whom, you can learn even more. E.g. Emmy Noether was a post-doc of David Hilbert in Goettingen, where other great mathematicians on the faculty included Felix Klein and Hermann Minkowski. And Klein and Lie were student friends who greatly influenced each other. Eventually I hope to tie this all into explaining how "Noether's theorem" as known to physicists is a pale shadow of the actual result, which belongs to Klein's theory of symmetries of differential equations (the ones generated by a Lagrangian).
Seriously, this is a rich resource for anyone interested in the history of physics (because so many mathematicians played a crucial role in physics via their mathematical insights).
Last edited: