- #1
zoltaaaan
- 2
- 0
Well hello there! :D
I'm doing a project on graphical simulation of a bullet hitting a glass plate, and I have some describing the way the shards fly off upon impact.
Note that in this calculation I am not yet taking the force of gravity or any forces other than the force of the impact of the bullet.
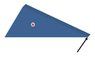
To be more precise, say my shard is a triangle-based prism as shown in the attached figure. If the bullet hit that shard at the center of its mass, perpendicularly to the plane of the base of the prism, the prism would - given that it doesn't break - receive some momentum and fly off straight along the axis of the initial trajectory of the bullet, without any rotation.
However, should the bullet hit anywhere beside the axis through the mass center of the shard, for example at one of its vertices, as shown on the figure, beside the straight translation, some rotation would also occur.
My question is: where is the axis of this rotation, and what forces (probably inertial) keep the other side of the shard in place.
I hope I made myself clear enough, if not, please let me know and I will try to elaborate further.
Thank you.
I'm doing a project on graphical simulation of a bullet hitting a glass plate, and I have some describing the way the shards fly off upon impact.
Note that in this calculation I am not yet taking the force of gravity or any forces other than the force of the impact of the bullet.
To be more precise, say my shard is a triangle-based prism as shown in the attached figure. If the bullet hit that shard at the center of its mass, perpendicularly to the plane of the base of the prism, the prism would - given that it doesn't break - receive some momentum and fly off straight along the axis of the initial trajectory of the bullet, without any rotation.
However, should the bullet hit anywhere beside the axis through the mass center of the shard, for example at one of its vertices, as shown on the figure, beside the straight translation, some rotation would also occur.
My question is: where is the axis of this rotation, and what forces (probably inertial) keep the other side of the shard in place.
I hope I made myself clear enough, if not, please let me know and I will try to elaborate further.
Thank you.
Attachments
Last edited: