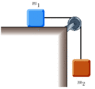
Solving the Tension in Connected Objects with Masses m1 and m2

[staz87]

Homework Statement

An object with mass m1 = 6.00 kg, rests on a frictionless horizontal table and is connected to a cable that passes over a pulley and is then fastened to a hanging object with mass m2 = 8.0 kg. Find the acceleration of each object and the tension in the cable.

Homework Equations

F=ma
A=T/6
"Need a Tension equation"

The Attempt at a Solution

I tried calculating the tension, T, but my book makes no specific mention of how one is to calculate it in this situation. I drew a free body diagram for the hanging object, and found that N=78.4. However I can't find the sum of forces in the y-directions since I am unable to find T.
Also I know that A(x) is equal to T, b/c there are no reactionary forces. If I could find T, I believe I could solve it.

Thanks in advance for your help!

 

[rootX]

first, analyze the external system. (Ignore *edit: tension*)
take into consideration only the forces acting on the ends **i meant like outside below m2 and to the left of m1**

and find net a of the system.

and then analyze any of those boxes...

 

[staz87]

first, analyze the external system. (Ignore *edit: tension*)
take into consideration only the forces acting on the ends **i meant like outside below m2 and to the left of m1**

and find net a of the system.

and then analyze any of those boxes...

What force exists to the left of M1?

 

[rootX]

that's null in this case.
but you know this is not always true.

 

[staz87]

that's null in this case.
but you know this is not always true.

Yes usually its friction right? So my 8-kg block, m2, should be accelerating at 9.8 m/s right? Is there a tension force pulling up on the block from m1? I am on webassign which allows for 5 submissions and 9.8 wasn't one of them

 

[rootX]

Yes usually its friction right? So my 8-kg block, m2, should be accelerating at 9.8 m/s right? Is there a tension force pulling up on the block from m1? I am on webassign which allows for 5 submissions and 9.8 wasn't one of them

yes, but just ignore it in this case.

your net external force for this system is wrong.

if m2 has a of 9.8 m/s then that would mean that

the force acting below m1 is 9.8*(m1+m2)

because net acc of the system should be equal to net ext force/total mass of the system

 

[Doc Al]

The most general way to approach this sort of problem is to analyze each block separately, then combine the results. Identify the forces acting on each block, then apply Newton's 2nd law. Since tension and acceleration are the unknowns that you are solving for, represent them symbolically. You'll get two equations--solve them together.

 

[staz87]

yes, but just ignore it in this case.

your net external force for this system is wrong.

if m2 has a of 9.8 m/s then that would mean that

the force acting below m1 is 9.8*(m1+m2)

because net acc of the system should be equal to net ext force/total mass of the system

Okay so this result yields 137. I am still confused as to what I use the answer for. Does it have something to do with the tension?

 

[staz87]

The most general way to approach this sort of problem is to analyze each block separately, then combine the results. Identify the forces acting on each block, then apply Newton's 2nd law. Since tension and acceleration are the unknowns that you are solving for, represent them symbolically. You'll get two equations--solve them together.

Okay so the 6.00 kg has a force T upon it in the +x direction.

8.00 kg has g*(6+8)= Force -y, but does it have a force T acting upon the 8 kg block in the
+y direction?

That's where I am confused If there is a force shouldn't there be a force in the opposite direction?

Now when I solve these equations you are talking about substitution where I solve for one variable then plug the solved variable into the other equation?

 

[learningphysics]

Okay so the 6.00 kg has a force T upon it in the +x direction.

8.00 kg has g*(6+8)= Force -y, but does it have a force T acting upon the 8 kg block in the
+y direction?

The 8kg force has its weight acting on it... and the tension... write out in the form $$\Sigma{\vec{F}}=ma$$

 

[Doc Al]

Okay so the 6.00 kg has a force T upon it in the +x direction.

Right!

8.00 kg has g*(6+8)= Force -y, but does it have a force T acting upon the 8 kg block in the
+y direction?

Since the string pulls up on it, there's a force T acting upward on m2. But the downward force on m2 due to gravity is just g*m2 = g*(8)---not g*(6+8).

That's where I am confused If there is a force shouldn't there be a force in the opposite direction?

Perhaps you're thinking of Newton's 3rd law, which certainly applies here just like everywhere else. For the tension it would work like this: The string pulls m2 with force T upward, thus m2 pulls the string with a force T downward. But all we care about to solve this problem are the forces on the two masses.

Now when I solve these equations you are talking about substitution where I solve for one variable then plug the solved variable into the other equation?

Exactly. Take care with your sign convention and constraint: If m1 moves to the right, m2 moves down.

 

[staz87]

Right!

Since the string pulls up on it, there's a force T acting upward on m2. But the downward force on m2 due to gravity is just g*m2 = g*(8)---not g*(6+8).


Perhaps you're thinking of Newton's 3rd law, which certainly applies here just like everywhere else. For the tension it would work like this: The string pulls m2 with force T upward, thus m2 pulls the string with a force T downward. But all we care about to solve this problem are the forces on the two masses.


Exactly. Take care with your sign convention and constraint: If m1 moves to the right, m2 moves down.

Ok so last question how do I find the force of tension acting upwards on M2? It would have to be tied to the 6kg weight correct? But since 6kg has no friction associated with its motion is it able to exert an opposite force on the Tension?

 

[learningphysics]

Ok so last question how do I find the force of tension acting upwards on M2?

It is the same tension acting on M1... write the f=ma equations for M1 and M2. Solve for tension.

It would have to be tied to the 6kg weight correct? But since 6kg has no friction associated with its motion is it able to exert an opposite force on the Tension?

There doesn't need to be friction for the 6kg mass to exert a force on the rope... it's just Newton's 3rd law.

 

[staz87]

It is the same tension acting on M1... write the f=ma equations for M1 and M2. Solve for tension.
QUOTE]


What is the acceleration on the 6kg block? is it 9.8m/s/s also?

 

[staz87]

Okay I assumed that M1 has a=9.8 as well. So I did m*a and got 58.4 N. Then M2, 8*9.8=78.4. So How do these forces interact. Does the 58.4 pull away from the 78.4 or do I add them together to get total tension? Still confused, sorry.

*Edit*

Okay just submitted that T in the cable was 19.6. I got this from 78.4-58.4=19.6 Should I add them?

 

[learningphysics]

It is the same tension acting on M1... write the f=ma equations for M1 and M2. Solve for tension.
QUOTE]


What is the acceleration on the 6kg block? is it 9.8m/s/s also?

No. And the 8kg mass doesn't accelerate at 9.8m/s^2 either.

you don't know what the acceleration is yet. Just use 'a'. If the 6kg block is accelerating to the right at 'a' m/s^2... then the 8kg block is accelerating downward at 'a' m/s^2...

You should get 2 equations with 2 unknowns (T and a).

 

[staz87]

*Solved*