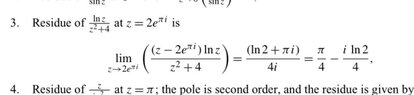Calculating Residue

[curious_mind]

Homework Statement:

Calculate the residue of the complex function $f(z) = \dfrac{\ln z}{z^2 + 4}$ at $z = 2 e^{i \pi}$

Relevant Equations:

$a = \lim_{z \rightarrow z_0} \left[ \left(z_0 - z\right) f(z) \right]$

This question is given as an example in the book by
Arfken, Weber, Harris, Mathematical Methods - a Comprehensive Guide, Seventh Edition.

It is solved as below attached in the image.

Can someone point it out how they proceed with calculations ? I do not seem to get their calculation.
I am aware $\ln z$ is a multivalued function. But at this point I do not know things about Branch points and etc.

According to my understanding the function is not singular at point $z=2 e^{i \pi} =−2$ . So why they have used limits ?

Am I missing something ? Please help.

Thanks.

 

[fresh_42]

I guess there is a typo and it should be $z_1=2e^{i \pi /2}.$

The formula goes
\begin{array}{c} \operatorname{Res}_{z_1}\left(\dfrac{h}{f}\right)=\dfrac{h(z_1)}{f'(z_1)} \end{array}

Reference: https://www.physicsforums.com/insights/an-overview-of-complex-differentiation-and-integration/

 

[curious_mind]

Even then, in numerator, it should be $\ln 2 + i \dfrac{\pi}{2}$ right ?

 

[vela]

I guess there is a typo and it should be $z_1=2e^{i \pi /2}.$

Or the denominator was supposed to be $z^2-4$. In either case, the example is all messed up.

 

[fresh_42]

Even then, in numerator, it should be $\ln 2 + i \dfrac{\pi}{2}$ right ?

Yes, ...

Or the denominator was supposed to be $z^2-4$. In either case, the example is all messed up.

... and yes.


At least, $2e^{i \pi /2}$ is a singularity. However, $z=-2$ would be faster to solve.