- #1
GreenPrint
- 1,196
- 0
Homework Statement
Find the length of the parabolic segment r = [itex]\frac{12}{1+cos(θ))}[/itex], 0[itex]\leq[/itex]θ[itex]\leq[/itex][itex]\frac{∏}{2}[/itex].
Homework Equations
L = ∫[itex]\sqrt{f(θ)^{2}+f^{'}(θ)^{2}}[/itex]dθ
The Attempt at a Solution
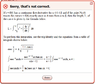
I got up to here and didn't know whta to do
L = 12 [itex]∫^{0}_{\frac{∏}{2}}[/itex] [itex]\frac{1}{1+cos(θ)}[/itex][itex]\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}[/itex]dθ
Wolfram alpha doesn't know neither
[itex]f(θ)^{2}[/itex] = [itex](\frac{12}{1+cos(θ))})^{2}[/itex]
[itex]f^{'}(θ)^{2}[/itex] = [itex](\frac{12sin(θ)}{(1+cos(θ))^{2}})^{2}[/itex]
[itex]\sqrt{f(θ)^{2}+f^{'}(θ)^{2}}[/itex] = [itex]\sqrt{(\frac{12}{1+cos(θ))})^{2}+(\frac{12sin(θ)}{(1+cos(θ))^{2}})^{2}}[/itex]=[itex]\frac{12}{1+cos(θ)}\sqrt{1+(\frac{sin(θ)}{1+cos(θ)})^{2}}[/itex]
Last edited: