Understanding Divisibility Rules: Proving 4 Does Not Divide n^2 + 5

[Instinctlol]

Prove: For all integer n, 4 does NOT divide n² + 5

The definition of | means the definition of divide.

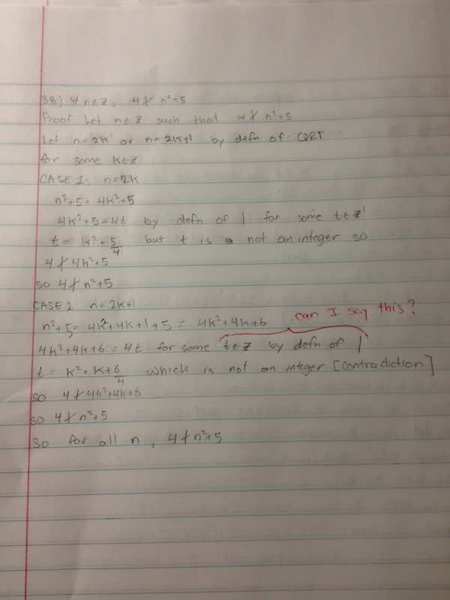
I need very thorough correction, down to the last support for every thing. Thank you

 

[Mark44]

You're doing more work than you need to.
For case 1, when n = 2k, you have n² + 5 = (2k)² + 5 = 4k² + 5 = 4(k² + 1) + 1. Clearly 4 | 4(k² + 1), but it can't also divide 4(k² + 1) + 1.

For case 2, use a similar argument.

 

[Bacle2]

I would state, re the first that from:

4k²+5=4t ,

you may also write:

5=4(t-k²) , for t,k² integers, which is not possible, i.e.,

5=4x has no solutions in integers (e.g. 4 is not invertible in integers.).

But that is a matter of preference (since I don't know the constraints; what you are or not allowed to work with).

To check possible congruences (mod4) , check the values (mod4) of each of the squares of : 4k, 4k+1,4k+2, 4k+3.

------------------------------

OR:

4|(n²+5) , then n²+5==0(mod4)→

n²==3mod4. But you can check that n²==0,1,2 but not 3 (mod4).

 

[Instinctlol]

But there is nothing wrong with my proof right?

 

[Deveno]

rather than use "not an integer" arguments, it would be cleaner to stay totally within the integers.

that is, if 4k²+ 5 = 4t

then 5 = 4(t - k²) → 4|5, impossible.

similarly, if 4k² + 4k + 9 = 4t

then 9 = 4(t - k² + k) → 4|9, also impossible.

*******

alternate proof # 1:

if 4|n² + 5, then n²+5 must be even, so n² must be odd → n is odd.

therefore n = 4k+1 or 4k+3 (all odd numbers are of one of these 2 forms).

(4k+1)² + 5 = 16k² + 8k + 6,

if this is divisible by 4, then 16k² + 8k + 6 = 4t, so

6 = 4(t - 4k² - 2k) → 4|6.

(4k+3)² + 5 = 16k² + 24k + 14, and as before:

16k² + 24k + 14 = 4t implies 14 = 4(t - 4k² - 6k),

so that 4|14, a contradiction.

*******

alternate proof #2:

let [a] = the residue class of a mod 4.

if 4|n² + 5, then [n² + 5] = [0], so [n²] = [-5] = [3].

but [n²] = [n][n] = [0][0], [1][1],[2][2], or [3][3].

[0][0] = [0] ≠ [3]
[1][1] = [1] ≠ [3]
[2][2] = [4] = [0] ≠ [3]
[3][3] = [9] = [1] ≠ [3],

so there is no n for which [n²] = [3], and so no n for which [n²+5] = [0], so 4 does not divide n²+ 5

********

why provide 3 proofs, when all you want to know is: is yours OK? hmm...it's a mystery, no? perhaps you think about it for a little bit.

 

[Instinctlol]

rather than use "not an integer" arguments, it would be cleaner to stay totally within the integers.

that is, if 4k²+ 5 = 4t

then 5 = 4(t - k²) → 4|5, impossible.

similarly, if 4k² + 4k + 9 = 4t

then 9 = 4(t - k² + k) → 4|9, also impossible.

*******

alternate proof # 1:

if 4|n² + 5, then n²+5 must be even, so n² must be odd → n is odd.

therefore n = 4k+1 or 4k+3 (all odd numbers are of one of these 2 forms).

(4k+1)² + 5 = 16k² + 8k + 6,

if this is divisible by 4, then 16k² + 8k + 6 = 4t, so

6 = 4(t - 4k² - 2k) → 4|6.

(4k+3)² + 5 = 16k² + 24k + 14, and as before:

16k² + 24k + 14 = 4t implies 14 = 4(t - 4k² - 6k),

so that 4|14, a contradiction.

why provide 3 proofs, when all you want to know is: is yours OK? hmm...it's a mystery, no? perhaps you think about it for a little bit.

I like the way you did the first two proofs, they look simple and to the point. I understand that there are many ways to do the same proof and it is always better to be able to write proofs efficiently because not all proofs are always this short.

I am reluctant to use your mod proof because we have not learned it that way. I have an exam coming up and I want to be able to just follow the professors style to get full points :tongue:

 

[Deveno]

I like the way you did the first two proofs, they look simple and to the point. I understand that there are many ways to do the same proof and it is always better to be able to write proofs efficiently because not all proofs are always this short.

I am reluctant to use your mod proof because we have not learned it that way. I have an exam coming up and I want to be able to just follow the professors style to get full points :tongue:

that is a fair point.. professors usually appreciate it when students don't "get ahead of themselves" and use theorems/concepts that haven't been covered yet.

that said, there's no harm in "looking ahead" and understanding that what you have done can be viewed an alternate way. it's like looking at two views of a 3-D object: one from the front, and one from the side. neither view is "wrong", but they are certainly different.

 

[Bacle2]

Proof seems correct; only thing is I don't know what you

are allowed to use (mostly: can you bring up rationals, or do you have to stay within

the integers?). If everything your using is allowed, it seems correct to me.