Unit Norm Axis Rotation in R3: Exploring Representation & Algebra

[LCSphysicist]

TL;DR Summary

I am having trouble to understand the reasoning that the author follows in these pages.

A rotation about an unit norm axis in R3

can be given by the following, that gives basically the elements of the matrix of the rotation: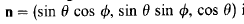

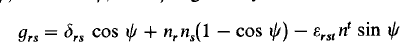
With these expression, we can obtain the three infinesimal rotations that corresponds to the three euler angles by first writing the three individuals matrix of these rotations, and then, taking the derivative:

Now, the autor gives the algebra regardind these transformations and talk about its representation in Rn

It is said that the representation A have the same algebra that g. And so he starts to talk about the canonical basis to represent as a way to write the representations.

After that, he returns to the beginning and says that

The relatios six and seven he says is that:

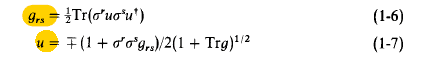
Now, i am extremelly confused about all this thing. More preciselly, i can't understand how 1.29 was obtained. It was used the A representation? How do he uses it? There is something to do with the canonical basis?

 

[Gaussian97]

Since you want to obtain a 2d representation, you need to use the representation with $2=2j+1$ i.e. $j=1/2$. Then the "canonical basis" is 2d and consists of $f_{-1/2}, f_{1/2}$. With eq. 1-28 you now know how $L_3$ and $L_{\pm}$ act on that base, and therefore you can construct the matrices in this base.
Now, knowing these 3 operators you can easily compute, using 1-26 the operators $A_i$. And from that, you can construct the unitary matrix.

 

[LCSphysicist]

Since you want to obtain a 2d representation, you need to use the representation with $2=2j+1$ i.e. $j=1/2$. Then the "canonical basis" is 2d and consists of $f_{-1/2}, f_{1/2}$. With eq. 1-28 you now know how $L_3$ and $L_{\pm}$ act on that base, and therefore you can construct the matrices in this base.
Now, knowing these 3 operators you can easily compute, using 1-26 the operators $A_i$. And from that, you can construct the unitary matrix.

Hello. Thank you. The real problem to me is, following your reasoning, make the last step. Tthat is, from the Ai obtained, how to construct the unitary matrix. How do exact we could do it? I am still new in these representations things, so i am a little confused about that.

 

[fresh_42]

Here is the theorem which classifies the finite-dimensional representations of $\{L_\pm ,L_3\}$:
https://www.physicsforums.com/insights/journey-manifold-su2-part-ii/ (section 7.1)

 

[Gaussian97]

Given the set of generators $A_i$, you can construct the elements of the group as
$$g(\alpha, \beta, \gamma) = \exp{(\alpha A_1 + \beta A_2 + \gamma A_3)}$$
Where the exponential must be understood as its Taylor expansion. The evaluation can be, in general, very difficult, fortunately for the 2d representation of SO(3) you can find easy expressions for the matrices $(\alpha A_1 + \beta A_2 + \gamma A_3)^n$ which allows you to write the exponential in the form 1-29