- #1
skrat
- 748
- 8
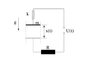
On conductive spring with constant k a plate o capacitor with mass [itex]m[/itex] and surface [itex]S[/itex] is hanged. It hangs [itex]x_{0}[/itex] above the second fixed plate. Determine average distance, frequency and max amplitude of distance between the plates in case of [itex]U(T)=Asin\omega t[/itex]. Say that capacity of capacitor is constant.
Ok, I tried like this but I found myself having some problems later in the process:
[itex]F_{c}+mg-kx=ma[/itex] where [itex]F_{c}[/itex] is the force between the capacitor's plates
[itex]F_{c}=e(t)E=F_{c}=e(t)E=\frac{e(t)^{2}}{\varepsilon _{0}S}[/itex] ([itex]E[/itex] comes from Gaussian law).
So now I have to found out how much e is on a plate at given t:
[itex]U(t)-IR-U_{C}=0[/itex]
[itex]U(t)-IR-\frac{e}{C}=0[/itex]
[itex]U(t)-IR-\frac{e}{C}=0[/itex]
[itex]\frac{U(t)}{dt}-R\frac{I}{dt}-\frac{1}{C}\frac{de}{dt}=0[/itex]
[itex]\frac{U(t)}{dt}-R\frac{I}{dt}-\frac{1}{C}I=0[/itex]
[itex]A\omega cos\omega t-R\frac{I}{dt}-\frac{1}{C}I=0[/itex]
Now I have no idea how to separate I and t, than integrate etc... :/
Ok, I tried like this but I found myself having some problems later in the process:
[itex]F_{c}+mg-kx=ma[/itex] where [itex]F_{c}[/itex] is the force between the capacitor's plates
[itex]F_{c}=e(t)E=F_{c}=e(t)E=\frac{e(t)^{2}}{\varepsilon _{0}S}[/itex] ([itex]E[/itex] comes from Gaussian law).
So now I have to found out how much e is on a plate at given t:
[itex]U(t)-IR-U_{C}=0[/itex]
[itex]U(t)-IR-\frac{e}{C}=0[/itex]
[itex]U(t)-IR-\frac{e}{C}=0[/itex]
[itex]\frac{U(t)}{dt}-R\frac{I}{dt}-\frac{1}{C}\frac{de}{dt}=0[/itex]
[itex]\frac{U(t)}{dt}-R\frac{I}{dt}-\frac{1}{C}I=0[/itex]
[itex]A\omega cos\omega t-R\frac{I}{dt}-\frac{1}{C}I=0[/itex]
Now I have no idea how to separate I and t, than integrate etc... :/