- #1
Wolvenmoon
- 11
- 0
Homework Statement
Consider a wet banked roadway, where there is a coefficient of static friction of 0.30 and a coefficient of kinetic friction of 0.25 between the tires and the roadway. The radius of the curve is R=50m
A: If the banking angle is β=25∘, what is the maximum speed the automobile can have before sliding up the banking? (Answer is in the low 20s)
B: What is the minimum speed the automobile can have before sliding down the banking?
(Answer is between 5-10 m/s)
Homework Equations
Newton's first law:
ƩF = 0 if a body is in equilibrium (at rest/constant velocity). This is per-axis.
Newton's second law (if accelerating)
ƩF = m*a
Magnitude of friction force:
f_fric (static or kinetic) = u*n where u is the coefficient of friction (either u_s or u_n) and n is the normal force.
Forces in uniform circular motion:
[itex]a_rad = \frac{v^2}{R} = \frac{4pi^2R}{T^2}[/itex]
The Attempt at a Solution
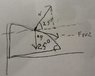
I'm reviewing this problem for an exam. I remember it was a beast. I'm having trouble figuring out how to do a free body diagram efficiently. I have dysgraphia and dyslexia - I've attached my work but I'm worried it might not be legible.
So essentially we're looking at a car on a wedge but our acceleration formula is different. The forces in the X direction include the centripetal force as well as the coefficient of static friction (the car is not moving in the X direction) times the amount of weight pressed against the wedge in the X direction.
The sum of the forces in the Y direction should be the coefficient of static friction (no movement on the Y axis) times the amount of weight still heading downwards.
For my free body diagram, I drew a right hand triangle with the hypotenuse facing right and the 90 degree angle at the origin. The car is a dot on this triangle. The angle β=25° is represented by the other corner of the triangle along the X axis.
Starting at the bottom and going counterclockwise.
The force mg is going straight down.
The force n is perpendicular to the hypotenuse of the triangle.
In part A the force of friction opposes the direction of movement, which is 'up' the banking angle. This makes the free body diagram of part A have the force of friction directed down the slope of the triangle.
Using this free body diagram, I am able to see that the Y component of weight is u_s * sin(25) * m. The x component should be u_s*cos(25)*m. Intuition says the Y component > the x component.
Checking this:
.30*sin(25)*1 = .1268
.30*cos(25)*1 = .2719
I've broken it here. However, my free body diagram shows that this should not be the case.
So I'm going to correct this - but I want to know why I have it wrong!
So the sum of the forces in the X direction is:
[itex]ƩF_x = m\frac{V^2}{R} + m u_s sin(25) = 0[/itex] (Equal to zero since the system is in equilibrium)
This is equal to
[itex]ƩF_x = m\frac{V^2}{50} + m .3 sin(25) = 0[/itex]
[itex]ƩF_x = \frac{V^2}{50} + .3 sin(25) = 0[/itex] (Mass factors out)
The sum of the forces in the Y direction is:
[itex]ƩF_y = m g + .3 m cos(25) = 0[/itex]
[itex]ƩF_y = g + .3 cos(25) = 0[/itex] (Mass factors out)
Equating these and solving for V, I get:
[itex]ƩF = \frac{V^2}{50} + .3 sin(25) = g + .3 cos(25) [/itex]
Solving this for V gets me very, very close to the answer for part A, but after rounding it is higher than the answer is. I tried using 9.8 and 9.81 for my values of g, but it isn't quite correct.
I'm going to continue because as I was typing this I realized I was very nearly getting it!
For part B, we're trying to avoid sliding down the embankment. Looking at part A's sums of the forces, for X we have mass times the centripetal acceleration plus the force resulting from gravity working in our favor. In part B, gravity is working against us. So...
For part A:
[itex]ƩF_x = m \frac{V^2}{50} + m .3 sin(25) = 0[/itex]
[itex]ƩF_y = m g + .3 m cos(25) = 0[/itex]
For part B, gravity is assisting the motion we do not want and is therefore negative/working against our positive forces (if someone could clarify this concept I would really appreciate it!)
[itex]ƩF_x = m \frac{V^2}{50} - m .3 sin(25) = 0[/itex]
[itex]ƩF_y = m g - .3 m cos(25) = 0[/itex]
Equating, dividing through by m:
[itex]ƩF = \frac{V^2}{50} - .3 sin(25)g = g - .3 m cos(25)[/itex]
Solving for V we get...the same answer as above? Hmmm. Well, .3*sin(25) and .3*cos(25) are very small numbers. So changing the signs doesn't really do much to gravity, which is huge in comparison. I am missing a multiplier.
...
Or I entered it into my calculator (useful when dealing with dysgraphia+dyslexia, perilous none-the-less) wrong and neglected gravity. Woe unto me.
Part A corrected:
[itex]ƩF = \frac{V^2}{50} + .3 sin(25) g = g + .3 cos(25) g [/itex]
Solving for V gives us the wrong value. Flipping trigonometric functions:
[itex]ƩF = \frac{V^2}{50} + .3 cos(25) g = g + .3 sin(25)*g [/itex]
Gets VERY CLOSE to the answer!
...switching to the coefficient of kinetic friction on the left side of the equation, the 'x' side, gets us to the answer.
[itex]ƩF = \frac{V^2}{50} + .25 cos(25) g = g + .3 sin(25) g [/itex]
Alright. Let's look at part B again. We're apparently still moving on the X axis.
Part B:
[itex]ƩF = \frac{V^2}{50} - .25 sin(25)g = g - .3 m cos(25) g[/itex]
Neither solving that nor this:
[itex]ƩF = \frac{V^2}{50} - .25 cos(25)g = g - .3 m sin(25) g[/itex]
for V yields the correct answer.
I've meandered enough and come VERY CLOSE to the answer, I think. What am I missing in part B?
Thanks!
Attachments
Last edited: