- #1
fluidistic
Gold Member
- 3,923
- 261
Homework Statement
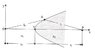
See the picture for the situation of the problem.
I'm told that any ray starting from S and getting through the "Cartesian Oval" reach point P.
I must show that the equation of the interface curve is [tex]l_0n_1+l_i n_2=K[/tex] where K is a constant.
So far I've showed that [tex]l_0=\sqrt {x^2+y^2}[/tex] and [tex]l_i=\sqrt {y^2+(s_0 + s_i -x)^2}[/tex]. But I remain stuck as how to proceed further.
Any idea is greatly appreciated.
Homework Equations
Snell's law? I've tried something with it but didn't reach anything.
Maybe Fermat's principle?
The Attempt at a Solution
See above.