- #1
BlasterV
- 38
- 0
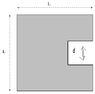
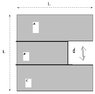
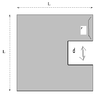
A uniform square plate L = 5.9 m on a side as a square section d = 2.5 m cut out of one side.
What is the center of mass of the remaining plate? Use a coordinate system with origin (0, 0) at the center of the plate.
The answer must be given in components.
X = ?
Y = ?. From the picture it is obvious the Y component is 0, so Y = 0 is correct. (and the auto-grade says correct also, so Y = 0 ).
However, exactly how to find the X component I can't figure out.
I tried 2-3 different ways of doing it, and none have worked, does anyone know exactly how to solve this problem for the X component? I tried a few things like splitting it up and using weighted averages but it is not working or I have the wrong equation.
Thanks! I am attaching a picture of the problem.
What is the center of mass of the remaining plate? Use a coordinate system with origin (0, 0) at the center of the plate.
The answer must be given in components.
X = ?
Y = ?. From the picture it is obvious the Y component is 0, so Y = 0 is correct. (and the auto-grade says correct also, so Y = 0 ).
However, exactly how to find the X component I can't figure out.
I tried 2-3 different ways of doing it, and none have worked, does anyone know exactly how to solve this problem for the X component? I tried a few things like splitting it up and using weighted averages but it is not working or I have the wrong equation.
Thanks! I am attaching a picture of the problem.