Find Center of Mass for Semicircular Wire

[Slightly]

Homework Statement

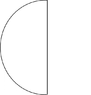
Find the center of mass of a semicircular wire. The wire is a semicircle, but the important thing to realize is that the wire is a closed loop. Think of a solid half disk, and just take the outer edge.
Where is the center of mass? This will be positioned with the center at the origin.
Radius b.

Homework Equations

cm = x1*m+x2*m/total mass

The Attempt at a Solution

What I tried to do was try to stay away from the integrals since there are just wires being used.
For the center of mass of x, it will be at zero because of symmetry.

For y, I used the equation above. With uniform density, the mass will factor out and I will just be left with lengths.

(2b*0 + Pi*b*2*b/Pi )/(2b + Pi*b)... is this right? or would you suggest that I use integrals.

 

[phinds]

Homework Statement

Find the center of mass of a semicircular wire. The wire is a semicircle, but the important thing to realize is that the wire is a closed loop. Think of a solid half disk, and just take the outer edge.

Self-contradictory. Doesn't make sense. Draw a picture.

 

[Slightly]

Here is the picture!

 

[phinds]

That makes sense. The wire is not a semi-circle, it is a semi-circle AND a connecting wire.

 

[paranormal]

Your approach is correct. Since the wire is a closed loop, we can use the concept of symmetry to determine the center of mass without using integrals.

As you mentioned, the center of mass in the x-direction will be at the origin due to the symmetry of the semicircle.

For the y-direction, we can use the equation you provided, where x1 and x2 represent the distances from the origin to the two points where the semicircle meets the x-axis. Since the semicircle has a radius of b, x1 and x2 will both be b. The total mass of the semicircle will be its length (which is 2b) times the linear density. Therefore, the center of mass in the y-direction will be (2b*0 + πb*2b)/(2b+πb) = πb/2.

So the center of mass for the semicircular wire will be at (0,πb/2) with respect to the origin.