Calculating Angle Theta in Centripetal Motion Problem

[strugglin-physics]

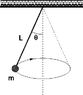
A mass m = 5.100 kg is suspended from a string of length L = 1.110 m. It revolves in a horizontal circle (see Figure). The tangential speed of the mass is 2.696 m/s. What is the angle theta between the string and the vertical (in degrees)?

My first question is what is tangential speed? Is that the V in the formula
Ac=v^2/r?

But my biggest problem (I think) is that I can't figure out how to draw a FBD for this picture.

Assistance is appreciated.

 

[Sirus]

Tangental (tangential? I dunno) speed is the magnitude of the velocity vector of the mass that points in a direction tangental to its circular path (that is, perpendicular to the centripetal force vector). It is the instantaneous speed of the mass. Yes, that formula is correct.

Kudos for starting with a free-body diagram. Think about all the forces present. What is the force causing the mass to stay in circular motion? What other force is present? Hint: neglecting friction, only two forces are acting on the mass.

 

[arildno]

To help you a bit further:
Note that the vertical component of the tension force must balance the weight of mass.

 

[strugglin-physics]

Is it a drag force? F=-bv and the weight force?

 

[e(ho0n3]

What drag force? There is no drag force in this problem?

 

[arildno]

Why do you think it is a drag force?

 

[arildno]

Let me help you out a bit:
1.The tension force is directed along the string, let it's magnitude be T.
2.Let $$\theta$$ be the angle you're supposed to find.
3. Hence, the vertical component of the tension force is $$T\cos\theta$$
4. This component must balance the weight of the mass, so we get from Newton's second law:
$$T=\frac{mg}{\cos\theta}$$
(No accelerations in the vertical)
5. The horizontal component of the tension force must provide the centripetal acceleration of the mass.
The radius R is evidently :$$R=L\sin\theta$$
Can you take it from here?

 

[strugglin-physics]

I don't know what the second force is... I know the weight force but I what is keeping the plane up can't be a contact force because it isn't touching anything. So that leaves magnetic or electric and I know it isn't either of those. Therefore, I'm stumped.

Sorry, totally thinking about the other problem. LOL :uhh:

 

[arildno]

The tension force is provided by the string.

 

[strugglin-physics]

So for the vertical component we have mg/cos theta times cos theta equals mass times acceleration. Don't the thetas cancel out and leave us with mg=ma making g = a
That doesn't help me figure out theta though, sigh, sorry for being such a pain... we have a test tomorrow... I have a funny feeling it is not going to be a really good day.

 

[arildno]

NO!
The vertical component of the tension force is, as I've said $$T\cos\theta$$
Then, look at the vertical component of Newton's 2.law:
$$T\cos\theta-mg=0$$
Hence, $$T=\frac{mg}{\cos\theta}$$

EDIT:
You are now done with finding the magnitude of the tension.
Use this expression for the magnitude of tension in the radial component of Newton's second law (in the horizontal plane, that is)

 

[arildno]

For your information, you should get:
$$\cos\theta=\sqrt{(1+(\frac{v^{2}}{2Lg})^{2})}-\frac{v^{2}}{2Lg}$$
where v is the tangential velocity.