Changing course of a satellite

[Karol]

Homework Statement

A satellite orbits, what should it do to move to a larger orbit (a greater radius)

Homework Equations

Velocity in orbit: $v=\sqrt{\frac{GM}{r}}$

The Attempt at a Solution

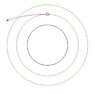
There are 2 options. the first, to my opinion, is to increase the velocity in the direction of travel, meaning forward. then it will go out of it's orbit, like in the drawing, and start making an ellipse.
When it reaches the outer orbit it has to slow down and to gain tangential velocity.
Because it's trajectory isn't round after it increased the speed, the radial gravity force slows it down, and it's possible to give it just enough more speed so it reaches the outer orbit with appropriate speed and will not need to be slowed down, just diverted.
The other possibility is to give it just enough radial speed to reach the outer orbit and then slow down the tangential velocity. i don't know which method is more economic.

 

[Karol]

kk

I forgot to attach the drwing

 

[Bandersnatch]

You started right, with a "prograde"(i.e., in the direction of the orbital motion) burn, but then it gets fuzzy.

It's probalby best to approach from the energy angle.

For clarity's sake, let's consider an elliptical orbit that's just right for the craft to reach the outer orbit at the farthest point of the ellipse.


When a craft is in a circular orbit with radius R, how much total energy does it have as compared to a craft in orbit R+ΔR?

When a craft is in an elliptical orbit that touches the orbit R at periapsis(the point of closest approach) and the orbit R+ΔR at apoapsis(the farthest point), how much total energy does it have at its closest and farthest points? Compare to the kinetic and potential energies of the corresponding circular orbits.

If at either of these two points, it'll turn out the kinetic energy of the craft in the elliptic orbit is higher than that of the circular one, it'll mean the engine burn has to be directed which way to change it from/to circular? And if it's lower?

We'll deal with your second approach later.

 

[dauto]

I don't like that question. What's the criteria? Should we try to

• Minimize the number of burns?
• Minimize the energy spent?
• Minimize the time spent?
• Minimize the complexity of the calculation?
• Something else?

 

[td21]

Sorry to interrupt, but does your question require "circular" orbit? If so, you may not consider increasing the velocity while the the satellite is orbiting, as the orbit could end up being elliptical.
My suggestion: Consider launching with higher velocity(energy).

 

[Karol]

If at either of these two points, it'll turn out the kinetic energy of the craft in the elliptic orbit is higher than that of the circular one, it'll mean the engine burn has to be directed which way to change it from/to circular? And if it's lower?

The mean potential energy in an ellipse is:
$$E_P=-\frac{GMm}{a}$$
where a is the long radius like in the drawing. the kinetic energy is inverse sign and half: $E_K=\frac{GMm}{2a}$, so for both R and R+ΔR it is smaller than in the circular orbit since R<a, so the velocities at the periapsis and apoapsis are smaller than those for circles, am i right?
So the burn must be backwards, to slow down, but it doesn't make sense since the potential energy is higher at R+ΔR, also the total energy which is:
$$E_{tot}=-\frac{GMm}{2r}$$
And we must invest energy, not to reduce it.

I am searching for the minimum energy solution, for now, i didn't know about all these options.

 

[Bandersnatch]

$a>R$ but $a<R+ΔR$ !
In your drawing, $R$ is represented by $r_1$ and $R+ΔR$ by $2a-r_1$. Earth is in the focus.

You'll see that the energy of the ellipse is more than the one, and less than the other. This implies that changing from circular orbit $R$ to ellipse $a$ (a>R) requires increase of energy, just as changing from $a$ to $R+ΔR$(a<R+ΔR).Rather than using mean energy, it might be more enlightening to do the following:

Write down $E_k+E_p$ for the object at:
1.circular orbit R
2.periapsis of the ellipse(distance R)
3.circular orbit R+ΔR
4.apoapsis (R+ΔR)

You'll notice that $E_p$ is equal for both #1 and #2 as well as #3 and #4(points where orbits touch). The only difference is in the kinetic energy.
To find out which case in each pair has more kinetic energy, consider the following - from centripetal acceleration considerations we can find out that the tangential velocity in circular motion is the minimum velocity sufficient to keep the object from falling down towards the source of gravity at a given distance.
So, if it's falling it's velocity(and kinetic energy) must be lower, than that required for circular motion, and if it's ascending, it must be higher. This tells you which way to aplly acceleration to circularise/decircularise the orbit.By the way, this might help gain an intuitive understanding of obital mechanics:
http://orbit.medphys.ucl.ac.uk/
It's an advanced, free spaceflight simulator. The manual covers basic(and not so basic) maneuvers. Pick the quick start scenario and try getting into orbit.
Nothing like learning by doing, although it does require some time investment to learn the controls.

 

[Karol]

At the periapsis $(R)$ the craft is falling toward earth, so the velocity decreases. it also comes out from my post that kinetic energy is $E_K=\frac{GMm}{2a}$. but we concluded that we have to add energy in order to enter the ellipse a, so how do we do it?
At the apoapsis $(R+ΔR)$ i have to increase velocity in order to enter the circular orbit $R+ΔR$ so it settles.

 

[Bandersnatch]

At the periapsis $(R)$ the craft is falling toward earth, so the velocity decreases.

No, at periapsis the craft has got too high a speed to stay in circular orbit at that distance. The craft is falling towards Earth at apoapsis.

Back to energies of the orbits - at periapsis(R), all the difference in energy between a circular orbit at R, and an elliptical orbit must come from kinetic energy(potential energy components being equal).
Same at apoapsis(R+ΔR) and the circular orbit (R+ΔR)

If the elliptical orbit has got more total energy than the corresponding circular one, then the craft must have had its kinetic energy increased to enter such an orbit. And vice versa.
You increase kinetic energy by accelerating, and decrease it by decelerating.

 

[rcgldr]

Two very short bursts are most efficient in terms of energy usage, but longer bursts are more practical in the case of limited thrust.

http://en.wikipedia.org/wiki/Hohmann_transfer_orbit