Charge of q Problem: Find q from Two 3.0g Spheres on 1.0m Threads

[Mindscrape]

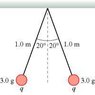
Two 3.0 g spheres on 1.0-m-long threads repel each other after being equally charged. What is the charge of q?

I don't know why I can't seem to get this right, but I am missing something somewhere. So, I figured I could find use the tension in the 1m string to find the horizontal component of the force, which would then equal the force of the repulsion between the charges. Which means that $$T_x = m g tan \theta$$. Also using trig to find the x leg yields .324m. If $$F = \frac{kq^2}{r^2}$$ then q should be $$q = \sqrt{\frac{mgtan\theta 2x^2}{k}}$$, and plugging in the numbers would be $$q = \sqrt{\frac{.003kg*9.8\frac{m}{s^2}*tan(20)*.684^2m}{(9*10^9\frac{Nm^2}{C^2})}}$$. But that gives that q=6.17*10^13C, which would be ripping atoms in air apart. Anyone chatch were I went wrong?

 

[Mindscrape]

Oh whoops, I just figured out what I did wrong. Usually instead of using division on my calculator I just tpye ^-1, but I forgot to. Nevermind, I was right.

 

[JosieNutter]

I worked this one out on my own and ended up with:

$$q = \sqrt{\frac{.003kg*9.8\frac{m}{s^2}*tan(20)*(2sin(20))^2 m}{(9*10^9\frac{Nm^2}{C^2})}}$$

(Which, as far as I can tell, is identical to the one above.)

It gives me an answer of 7.46*10^-7... which is apparently incorrect. What am I missing here? I keep coming up with the same equation no matter how I approach the problem. This is super frustrating.

 

[JosieNutter]

Er... nevermind. I finally realized it was asking for nC - not C. Big difference in numbers there. :p