- #1
Saitama
- 4,243
- 93
Homework Statement

Following are the questions based on the above paragraph
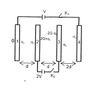
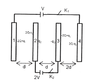
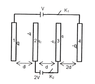
Q1)The charge appearing on the outer surface of plate 1, when switches K1 and K2 are open
A)zero
B)Q
C)-Q
D)-3Q
Q2)If K1 is closed and K2 is open, the charge appearing on the right surface of plate 2 is
A) ##Q/2+(\epsilon_0A/d)V/4##
B)##(\epsilon_0A/d)V/4+3Q/2##
C)##(\epsilon_0A/d)V/4-Q/2##
D)##3Q/2##
Q3)If both switches are closed, the charge appearing on plate 4 is
A)##(\epsilon_0A/d)V##
B)##(\epsilon_0A/d)V/2+Q##
C)##Q-(\epsilon_0A/d)V/2##
D)##(\epsilon_0A/d)V/3##
For Q1), it can be easily done by equating the electric field at any point inside the plate equal to zero but the solution solves it in a single line. It is written that "Charge on outermost surface=(net charge on system/2)=0". How did it arrive at this result?
About Q2) and Q3), I have no idea. I am clueless on how to even begin with them.
Any help is appreciated. Thanks!
Following are the questions based on the above paragraph
Q1)The charge appearing on the outer surface of plate 1, when switches K1 and K2 are open
A)zero
B)Q
C)-Q
D)-3Q
Q2)If K1 is closed and K2 is open, the charge appearing on the right surface of plate 2 is
A) ##Q/2+(\epsilon_0A/d)V/4##
B)##(\epsilon_0A/d)V/4+3Q/2##
C)##(\epsilon_0A/d)V/4-Q/2##
D)##3Q/2##
Q3)If both switches are closed, the charge appearing on plate 4 is
A)##(\epsilon_0A/d)V##
B)##(\epsilon_0A/d)V/2+Q##
C)##Q-(\epsilon_0A/d)V/2##
D)##(\epsilon_0A/d)V/3##
Homework Equations
The Attempt at a Solution
For Q1), it can be easily done by equating the electric field at any point inside the plate equal to zero but the solution solves it in a single line. It is written that "Charge on outermost surface=(net charge on system/2)=0". How did it arrive at this result?
About Q2) and Q3), I have no idea. I am clueless on how to even begin with them.
Any help is appreciated. Thanks!