- #1
Dunder
- 4
- 0
Homework Statement
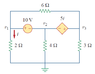
Find v1, v2, v3
Must be done with nodal analysis
Homework Equations
I=V/R
The Attempt at a Solution
So i started by saying i1 = v2/4, i = v1/2, i3 = v3/3
i + i1 + i2 = 0
v3-v2=51
v1-v2=0
I am not really sure to what to do from here, i can't seem to come across the right solution, the answer given in the book is v1=3.043, v2=-6.956, v3=0.6522
Any help would be much appreciated