Circuits and Resistance

[disneychannel]

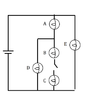
When the switch is closed, what happens to the brightness of bulb D? What happens to the brightness of bulb A? Explain your reasoning.

I initially thought it would decrease because current splits between D and BC. But since it is parallel to BC would it increase because the it would be R/2 instead of R? And will A stay the same?

 

[disneychannel]

OR does everything just get brighter?

 

[Simon Bridge]

What determines how bright a particular bulb is?

 

[disneychannel]

Current and resistance

 

[Drakkith]

Let's assign some resistance values and voltage. Let's say that every bulb has a resistance of 10 ohms and the voltage is 10 volts. Now, find the current and voltage drop across each bulb before and after the switch is closed. Do you know how to do that?

 

[B4ssHunter]

notice that when you connect a resistor in parallel , it gets a lower value than the value of the resistance itself
that means if you have one 2 ohm resistor , there you go you have 2 ohms of resistance , but if you connect 2 ohms with another 2 ohms in parallel , you get a 1 ohm equivalent resistance , when you close the switch , D is now parallel connected with B and C , thus it has lower resistance
everything lights up because now you have a lot less equivalent resistance , so more current is present
but also current is split up between D and b - c
i think that the current split over comes the decrease in resistance thus decreasing the its intensity , but E surely gets brighter , A surely gets brighter , D gets dimmer if they all have the same resistance

 

[B4ssHunter]

What determines how bright a particular bulb is?

current intensity

 

[Drakkith]

when you close the switch , D is now parallel connected with B and C , thus it has lower resistance
everything lights up because now you have a lot less equivalent resistance , so more current is present

Have you done the math? It will show you that this is not exactly true.

 

[disneychannel]

that means the current is 1 for everything...

 

[Drakkith]

that means the current is 1 for everything...

Remember that D and A are in series, and their resistance adds together.

 

[Simon Bridge]

Current and resistance

Hmmm... sort of, but how?
If I double the resistance but halve the current will that make the bub brighter or dimmer?
Is there a single quantity that the bulb brightness is related to?

In this case you can probably get away with modelling all the resistances as a single value ... so if I double the current and keep the resistance the same, what happens to the brightness? Do you know how to calculate the current through the bulb in each case?

Like Drakkith is pointing out, it is possible to do this by rules of thumb: looking at the possible paths for the current in both cases. This requires you to understand how electric circuits work. When you don't have this understanding, you have to do it the hard way :(

Note: I'm just going to let him talk to B4ssHunter. "Current Intensity" is the old name for "Electric Current" which we just shorten to "Current".

 

[disneychannel]

BCDE would have 1/3 resistance so 3 times the current

 

[disneychannel]

Thinking the basic way i just though a would be the same and d would be dimmer. but thinking quantitatively i got confused

 

[TurtleMeister]

[STRIKE]It does not[/STRIKE]. Remember that D and A are in series, and their voltage will be split while their current is shared.

Edit: Sorry, when the switch is open the current will be 1 amp through A, D and E. What will happen when the switch is closed?

Assuming values are set per your post #5, shouldn't that be 0.5 amp for A and D, and 1 amp for E? A and D in series is 20 ohms.

 

[Drakkith]

Assuming values are set per your post #5, shouldn't that be 0.5 amp for A and D, and 1 amp for E? A and D in series is 20 ohms.

Ah! That's what I get for second guessing myself!

Plus the 2 hours of math homework I've already done.

 

[B4ssHunter]

Have you done the math? It will show you that this is not exactly true.

yes i know D dims out, i have mentioned this in the end of my comment

 

[Simon Bridge]

BCDE would have 1/3 resistance so 3 times the current.

How do you get that?

Thinking the basic way i just though a would be the same and d would be dimmer. but thinking quantitatively i got confused

If you show me your calculation, I may be able to help with that.
It would also help if you answered the questions put to you in the thread.

I have a feeling you are not the only one getting confused ;)

 

[disneychannel]

notice that when you connect a resistor in parallel , it gets a lower value than the value of the resistance itself
that means if you have one 2 ohm resistor , there you go you have 2 ohms of resistance , but if you connect 2 ohms with another 2 ohms in parallel , you get a 1 ohm equivalent resistance , when you close the switch , D is now parallel connected with B and C , thus it has lower resistance
everything lights up because now you have a lot less equivalent resistance , so more current is present
but also current is split up between D and b - c
i think that the current split over comes the decrease in resistance thus decreasing the its intensity , but E surely gets brighter , A surely gets brighter , D gets dimmer if they all have the same resistance

So since A= BCD. it wil be brighter. and since the current is split between that then half goes to D then half goes to BC. so that's how you get it. But E would stay the same I believe because it is its own independent pathway...?

 

[Drakkith]

BCDE would have 1/3 resistance so 3 times the current

E is in parallel with everything else and has nothing in series. Therefor the voltage across it is always 10 volts. As such, closing the switch will do nothing to it. The current will remain at 1 amp.

A and D are in series, with 10 ohms of resistance. This adds to 20 ohms for a current of 0.5 amps through their leg of the circuit.

Now, when the switch closes, we have 2 more bulbs added that are in series with each other, parallel to D, and in series with A. The resistance of leg BC is 20 ohms.

Now we find the equivalent resistance for BCD, and after knowing that we can figure out the voltage drop across A and BCD and the current flow through that leg (all of which passes through A). THEN knowing the voltage drop across BCD, we can find out how much current is going through BC and D.

At that point you will have the current through each bulb.

(It's been a while since I took my basic electronics course, so someone correct me if I'm wrong)

 

[B4ssHunter]

according to my calculations , when the switch is closed , total resistance decrease thus current increases , but also the resistance of the first branch drastically decrease so it takes more current so it dims E , only A would be brighter D dims and ofcourse the other two bulbs would just light up

 

[Drakkith]

So since A= BCD. it wil be brighter. and since the current is split between that then half goes to D then half goes to BC. so that's how you get it. But E would stay the same I believe because it is its own independent pathway...?

BC is twice the resistance of D and will not get half the current through that leg.

 

[Drakkith]

according to my calculations , when the switch is closed , total resistance decrease thus current increases

TOTAL current is irrelevant for this problem.

but also the resistance of the first branch drastically decrease that takes more current such that it dims E , only A would be brighter D dims and ofcourse the other two bulbs would just light up

No, the voltage applied to E remains at 10 volts, just as the voltage across leg ABCD is 10 volts. Since you have 10 volts applied to 10 ohms, you have 1 amp of current across E at all times.

 

[B4ssHunter]

TOTAL current is irrelevant for this problem.



No, the voltage applied to E remains at 10 volts, just as the voltage across leg ABCD is 10 volts. Since you have 10 volts applied to 10 ohms, you have 1 amp of current across E at all times.

i used another set of calculations not the ones you are using

 

[B4ssHunter]

TOTAL current is irrelevant for this problem.



No, the voltage applied to E remains at 10 volts, just as the voltage across leg ABCD is 10 volts. Since you have 10 volts applied to 10 ohms, you have 1 amp of current across E at all times.

yes the voltage remains the same , but the branch now has less resistance , so more current goes through the branch , even though since the total resistance decreased more current goes through E , but it does not compensate the loss of current in E resistor due to the decrease in resistance in the branch
* i took different values for the resistors and voltage , i think it depends on the values then *

 

[Simon Bridge]

So since A= BCD. it wil be brighter. and since the current is split between that then half goes to D then half goes to BC. so that's how you get it. But E would stay the same I believe because it is its own independent pathway...?

That's right, E stays the same.

But I don't know what you mean by "A=BCD".
However: the current only splits in half if there is equal resistance on both sides.

Note: if you don't answer questions I cannot help you.

 

[B4ssHunter]

That's right, E stays the same.

But I don't know what you mean by "A=BCD".
However: the current only splits in half if there is equal resistance on both sides.

Note: if you don't answer questions I cannot help you.

how does E stay the same ? when the parallel resistors were connected , the whole resistance of the branch was decreased , thus more current would flow through the branch and less current would flow through E , even if the intensity went a little bit higher due to the total decrease in resistance

 

[Drakkith]

yes the voltage remains the same , but the branch now has less resistance , so more current goes through the branch , even though since the total resistance decreased more current goes through E , but it does not compensate the loss of current in E resistor due to the decrease in resistance in the branch

E's resistance is NOT changing.

 

[Drakkith]

how does E stay the same ? when the parallel resistors were connected , the whole resistance of the branch was decrease , thus more current would flow through the branch and less current would flow through E , even if the intensity went a little bit higher due to the total decrease in resistance

You're coming at this from the wrong angle. Do not look at resistance changing. The resistance of any component will NOT change.

As such, if the resistance of E doesn't change, and the voltage drop (which is equal to the applied voltage) doesn't change, then current flow MUST stay the same through E.

 

[B4ssHunter]

E's resistance is NOT changing.

i know it doesn't
but i apologize i made a stupid mistake , i am sorry again

 

[B4ssHunter]

You're coming at this from the wrong angle. Do not look at resistance changing. The resistance of any component will NOT change.

As such, if the resistance of E doesn't change, and the voltage drop (which is equal to the applied voltage) doesn't change, then current flow MUST stay the same through E.

btw when i said the branch i meant the one without the E , the one containing a , b , c and D . not E i know E is not changing

 

[2milehi]

I assigned the voltage to V and the resistance of each light to R. Using V = I * R, parallel resistance equivalence, and current division I was able to algebraically determine current through the ABCD leg and then the voltage drop through A and D.

Skip intuition on this one it trips you up.

 

[Simon Bridge]

Skip intuition on this one it trips you up.

I noticed that too - both the current and the voltage changes.

What I have been trying to get OP to realize is that it is the power dissipated in the bulb that determines the brightness. This is proportional to the square of the current or the inverse square of the voltage.

Since the possible answers are:
brighter,
dimmer,
stays the same
... there is a 1/3 chance of getting the right answer just by guessing.
It follows that the reasoning that is followed needs to be clear and correct to get good marks.