Are my capacitor connections correct?

[pyroknife]

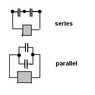
When you connect 2 capacitors together, how do you know if you connect them in series/parallel?

One of my problems was to connect 2 capacitors with positive to positive and negative to negative ends connected. That came out to be a series drawing.
Another problem was to connect 2 capacitors with positive to negative. That came out to be a parallel circuit.

So if you connect 2 positives together it = series circuit? A + & - connected = parallel?

 

[MetalManuel]

When capacitors are in series, there is an induced charged (polarization) in between the two capacitors. When capacitors are in parallel the charge is evenly distributed among the capacitors (no induced charge). For example, you can look at a dielectric in between a capacitor that is smaller than the space as a 2 capacitors in series due to the induced polarization on the dielectric.

 

[pyroknife]

A 12-μF capacitor and a capacitor of unknown capacitance are both
charged to 2.00 kV. After charging, the capacitors are disconnected from the
voltage source. The capacitors are then connected to each other⎯positive plate to
negative plate and negative plate to positive plate. The final voltage across the
12-μF capacitor is 1.00 kV. (a) What is the capacitance of the second capacitor?
(b) How much energy was dissipated when the connection was made?

For this problem they connected the 2 capacitors as a parallel circuit, I don't understand why it works like that.

 

[ehild]

Series or parallel connection are meant with respect to the other part of a circuit. The series connection means that one terminal of both elements is common (and nothing else is connected to this common point) and the free terminals are connected to the other part of the circuit. Parallel connection means that both terminals are common and these common points join to the other part of the circuit. See attached picture.
In your problem, both terminals of the capacitors were common and connected to a voltmeter. The grey block in the drawing is a voltmeter. With respect to the meter, the capacitors are parallel connected.

ehild

 

[pyroknife]

Series or parallel connection are meant with respect to the other part of a circuit. The series connection means that one terminal of both elements is common (and nothing else is connected to this common point) and the free terminals are connected to the other part of the circuit. Parallel connection means that both terminals are common and these common points join to the other part of the circuit. See attached picture.
In your problem, both terminals of the capacitors were common and connected to a voltmeter. The grey block in the drawing is a voltmeter. With respect to the meter, the capacitors are parallel connected.

ehild

I think I understand the series&parallel circuits, but I'm just lost on the problem.For my problem, how do you know that both terminals of the capacitors are common?

 

[ehild]

I think I understand the series&parallel circuits, but I'm just lost on the problem.For my problem, how do you know that both terminals of the capacitors are common?

The capacitors are then connected to each other, positive plate to
negative plate and negative plate to positive plate. The final voltage across the 12-μF capacitor is 1.00 kV.

Does that not mean that the capacitors have two pairs of terminal in common? Positive plate of the first one is connected to the negative plate of the second and the negative plate of the first one is connected to the positive plate of the second one.

Calculate both the initial and final charge on the 12 μF capacitor, Qi and Qf.
The initial charge on the other one is qi and the final is qf.

Both the initial and the final voltages are the same for both capacitors.

When the capacitors are connected - positive plate to the negative one -, part of the charges neutralize, and the magnitude of the overall net charge is |Qi-qi|=Qf+qf.

Substitute for qi and qf in terms of the voltages and the capacitance of the second capacitor.

ehild

 

[pyroknife]

Does that not mean that the capacitors have two pairs of terminal in common? Positive plate of the first one is connected to the negative plate of the second and the negative plate of the first one is connected to the positive plate of the second one.

Calculate both the initial and final charge on the 12 μF capacitor, Qi and Qf.
The initial charge on the other one is qi and the final is qf.

Both the initial and the final voltages are the same for both capacitors.

When the capacitors are connected - positive plate to the negative one -, part of the charges neutralize, and the magnitude of the overall net charge is |Qi-qi|=Qf+qf.

Substitute for qi and qf in terms of the voltages and the capacitance of the second capacitor.

ehild

So if the problem had been to connect positive to positive and negative to negative it would still have 2 terminals in common, correct? Also for the lQi-qil=Qf+qf. I don't understand that part, I saw that in the solutions manual too. When you apply conservation of charge shouldn't you have before=after which would be Qi+qi=Qf+qf? Why's the negative charge in there? Is the initial charges when they're not connected?

 

[ehild]

So if the problem had been to connect positive to positive and negative to negative it would still have 2 terminals in common, correct? Also for the lQi-qil=Qf+qf. I don't understand that part, I saw that in the solutions manual too. When you apply conservation of charge shouldn't you have before=after which would be Qi+qi=Qf+qf? Why's the negative charge in there? Is the initial charges when they're not connected?

The charge of a capacitor is given by a positive number. When you say that the charge of a capacitor is Q1=10 mC it means that 10 mC charge is on one plate and -10 mC is the charge on the other one.
If you have an other capacitor charged to Q2=12 mC and connect them, plus plate to plus, minus plate to minus, the net charge will be Q1+Q2=22 mC on one plate and -Q1-Q2=-22 mC on the other one. When you connect plus plate to minus, the charges add again, but one charge is positive and the other is negative, so you get 12μF - 10μF =2μF on one plate and -12μF + 10μF=2μF on the other one.

When you connect the plates with opposite polarity Qi-qi charge is left. This charge is shared between the capacitors, but he connected plates have the same polarity. Both charges are positive at one pair of plates of the connected capacitors, and negative on the other ones, so the net charge on the plates is Qf+gf and -(Qf+gf).

ehild

 

[pyroknife]

The charge of a capacitor is given by a positive number. When you say that the charge of a capacitor is Q1=10 mC it means that 10 mC charge is on one plate and -10 mC is the charge on the other one.
If you have an other capacitor charged to Q2=12 mC and connect them, plus plate to plus, minus plate to minus, the net charge will be Q1+Q2=22 mC on one plate and -Q1-Q2=-22 mC on the other one. When you connect plus plate to minus, the charges add again, but one charge is positive and the other is negative, so you get 12μF - 10μF =2μF on one plate and -12μF + 10μF=2μF on the other one.

When you connect the plates with opposite polarity Qi-qi charge is left. This charge is shared between the capacitors, but he connected plates have the same polarity. Both charges are positive at one pair of plates of the connected capacitors, and negative on the other ones, so the net charge on the plates is Qf+gf and -(Qf+gf).

ehild

Thanks. I getwhere the left hand side of that eq came from now. Is the right hand side always the sum of the positive charges? and can you answer this "So if the problem had been to connect positive to positive and negative to negative it would still have 2 terminals in common, correct?" I will check back tomorrow, thanks again.

 

[ehild]

The charge of the capacitor is meant a positive number. I used the absolute value of the difference of charges on the left hand side, as we do not know which of Qi and qi are greater. Both sides of the equation are positive (or zero).

If you connect both terminals of something to the terminals of an other thing, both things will have two terminals in common.
Holding a flower in both your hands, you grab both hands of a girl, then both of you have two flowers in common.

 

[pyroknife]

The charge of the capacitor is meant a positive number. I used the absolute value of the difference of charges on the left hand side, as we do not know which of Qi and qi are greater. Both sides of the equation are positive (or zero).

If you connect both terminals of something to the terminals of an other thing, both things will have two terminals in common.
Holding a flower in both your hands, you grab both hands of a girl, then both of you have two flowers in common.

Ugh I still don't get why the right hand side is Qf+qf

 

[ehild]

Ugh I still don't get why the right hand side is Qf+qf

What else should it be? What do you think? Both capacitors have some charge finally. The plates connected are at the same potential, so the charges on them are of the same sign.

ehild

 

[pyroknife]

What else should it be? What do you think? Both capacitors have some charge finally. The plates connected are at the same potential, so the charges on them are of the same sign.

ehild

In my problem tho, when you form Ceq. Shouldn't one plate be Qi-qi and the other be qi-Qi because that's how they're connected?

 

[ehild]

In my problem tho, when you form Ceq. Shouldn't one plate be Qi-qi and the other be qi-Qi because that's how they're connected?

You are right, when connecting the capacitors, the net charge on one pair of connected plates is Qi-qi, and the opposite, -(Qi-qi) =qi-Qi on the other one.

ehild

 

[pyroknife]

You are right, when connecting the capacitors, the net charge on one pair of connected plates is Qi-qi, and the opposite, -(Qi-qi) =qi-Qi on the other one.

ehild

There is something I have to be overlooking, probably something easy. In the solution manual they drew ceq as Qi-qi on 1 plate and Qi+qi on the other plate, which I have no idea where they got that from. So I thought that's how they applied conservation of charge by setting 1 plate = to the other. But the other plate should be qi-Qi. I attached a link.

 

[pyroknife]

It is a misprint in the manual.

ehild

In other words does it mean that conservation of charge for this problem is the magnitude of the sum of charges of 1 plate of capacitors set equal to the sum of the 2 positive charge on the 2 capacitors and NOT one plate of Ceq set equal to the other plate of Ceq?

 

[Phrak]

"Series" or "parallel" designations are not absolute, but are with respect to two nodes.

 

[ehild]

I just looked at the manual more carefully. It does not say that there is Qi-qi charge on one plate of the equivalent capacitor and Qi+qi charge on the other plate. It is written Qf+qf, which is not consistent with the next equation as it suggests that there are equal charges on both plates. One plate has to be positive, the other is negative. The magnitude of the charge is the same on both plates, but the sign are opposite. The charge is qi-Qi on the other plate, which is the same as -(Qf+qf).

The further part of the solution is correct. It solves the equation Qi-qi=Qf+qf, by using the relation Q=CV.

ehild