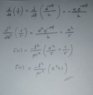- #1
cemtu
- 99
- 7
- Homework Statement
- In polar coordinates find the force as a function of radial coordinate F(r) that allows a particle to move in logarithmic spiral orbit r=k*e^(α*θ) , where k and a are constants.
- Relevant Equations
- ## \frac{d^2}{dθ^2}(1/r)+1/r=(-μr^2)⋅F(r)/l^2 ##
I believe I solved this. Is this solution true? Can please anyone just check?