- #1
deenuh20
- 50
- 0
Homework Statement
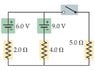
Two batteries and three resistors are connected as shown in the figure. How much current flows through the 9.0 V battery?
(a) When the switch is closed?
(b) When the switch is open?
Homework Equations
Kirchhoff's Loop Rule
I=V/R
The Attempt at a Solution
To find the current when the circuit is open, I totally disregarded the 5 ohm resistor and found the equivalent resistors of 2 and 4 and got 6. Then I used the equation I=9V/6 and that didn't work.
For the current when the circuit is closed, I applied Kirchhoff's Loop rule and found the current for each loop then solved by adding the two. That didn't work so I redrew the diagram and placed the 5 ohm resistor between the 2 and 4 ohm resistor and tried to figure out the current of that loop, but it also didn't work.
Additionally, does the 6 V battery in the drawing have anything to do with achieving the correct answer?
Thank you very much.