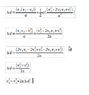Combining Equations: A Guide for Solving Complex Problems

[aboojoo]

Unsure of how to start the algebraic process of combining these two equations:


v₂=v₁+aΔt and Δd=v₁Δt+1/2aΔt² ,


The attached is a screenshot of the course material that I need help with. It demonstrates how to combine the two equations but it seems to skip some steps that I can't quite catch. I gathered to do so I should substitute one equation into the other, but do not know where to start. Some guidance would be greatly appreciated. Thank you

 

[jackarms]

I think it helps to know first the goal for combining two, and that is to eliminate a variable. You could eliminate any of the variables in either equation, but in the picture you posted they eliminate Δt, so that's where you would start to combine them. One way would be to solve for Δt in one equation and then substitute into the other. That's essentially what they did, except by manipulating the left side to then substitute in something else.

 

[aboojoo]

Could you show me the exact algebraic steps involved?
Not sure where the 2a(v₁Δt) comes from.

 

[jackarms]

Well, if you solve for $\Delta t$ in the first equation, you get: $$\Delta t = \frac{v_{2} - v_{1}}{a}$$
Substituting into the second equation yields: $$\Delta d = v_{1} \cdot \frac{v_{2} - v_{1}}{a} + \frac{1}{2}a \cdot (\frac{v_{2} - v_{1}}{a})^{2}$$

See if you can simplify from there.

 

[aboojoo]

I think I understand now, but am still puzzled by how the original text managed to get to the answer by simply squaring both sides of v2=v1+aΔt. It is a method I'm unfamiliar with since I do not know those steps.

I attached a picture for the rest of the steps that were to be done after yours. Thanks a lot for your help!*Edit, Spelling

 

[jackarms]

No problem -- glad you were able to work it all out. Don't be discouraged about how the text got the answer. Combining equations is somewhat of an art form. The simplest way is usually to do a substitution like I showed you, but there are other ways like those the text used that involve cleverly cancelling certain things out to get the answer in fewer steps. For anyone to see immediately how to combine two equations as they did would be quite astounding.