- #1
OhNoYaDidn't
- 25
- 0
Homework Statement
With
Homework Equations
So.. This was in my Complex Analysis exam, and i have no idea what to do. I always seem to get stuck at these more abstract questions.
I tried to fix it.OhNoYaDidn't said:Homework Statement
With. Give an example, if it exists, of a non constant holomorphic function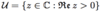 that returns zero in all points, and has the form 1/n, where n € N.
that returns zero in all points, and has the form 1/n, where n € N.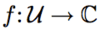
Homework Equations
So.. This was in my Complex Analysis exam, and i have no idea what to do. I always seem to get stuck at these more abstract questions.
Complex analysis is a branch of mathematics that deals with the study of complex numbers and their functions. It is the study of the properties and behavior of complex-valued functions, which are functions that take complex numbers as inputs and produce complex numbers as outputs.
Complex analysis has a wide range of applications in mathematics and science. It is used in physics, engineering, computer science, and other fields to model and solve problems involving complex systems. It is also used in number theory, geometry, and other areas of pure mathematics.
Some key concepts in complex analysis include analytic functions, complex integration, Cauchy's integral theorem, and the Cauchy-Riemann equations. Other important ideas include Laurent series, residue theory, and conformal mapping.
Complex analysis and real analysis are both branches of mathematical analysis, but they focus on different types of numbers. Real analysis deals with functions of real numbers, while complex analysis deals with functions of complex numbers. Additionally, complex analysis introduces new concepts such as analyticity and holomorphicity, which have no analogues in real analysis.
Some common techniques for solving complex analysis problems include using Cauchy's integral formula, the Cauchy-Riemann equations, and the residue theorem. Other useful tools include the Cauchy integral theorem, the maximum modulus principle, and conformal mapping techniques.