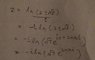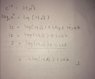Exploring the World of Complex Numbers: Beginners Guide

[MissP.25_5]

Hello,
please I need help. I have no idea how to start this. Can someone guide me? This is not homework, I'm just studying on my own and I really don't know how to begin this.

 

[benorin]

probably ought to start with $\cos z = \frac{1}{2}\left(e^{iz}+e^{-iz}\right)$, substituting into the given equation we have

$$\frac{1}{2}\left(e^{iz}+e^{-iz}\right)=2$$

now multiply both sides by $2e^{iz}$ and collect all the terms on one side...

 

[MissP.25_5]

probably ought to start with $\cos z = \frac{1}{2}\left(e^{iz}+e^{-iz}\right)$, substituting into the given equation we have

$$\frac{1}{2}\left(e^{iz}+e^{-iz}\right)=2$$

now multiply both sides by $2e^{iz}$ and collect all the terms on one side...

Why must we multiply both sides by $2e^{iz}$ ?

 

[Nick O]

Do it, and see what you end up with. I think you'll agree that it becomes much easier find the set of solutions for z.

 

[MissP.25_5]

Do it, and see what you end up with. I think you'll agree that it becomes much easier find the set of solutions for z.

Is this ok?

 

[Nick O]

Very close! You're just missing one part to capture the periodic nature of cosine.

 

[MissP.25_5]

Very close! You're just missing one part to capture the periodic nature of cosine.

Which part? I don't understand. I thought that would be enough?

 

[Nick O]

If cos(z) = 2, what is cos(z+2pi)?

 

[Nick O]

I'll be honest and say that I don't know how to produce the extra term from that particular solution, but that's only because I'm missing something that someone else will probably pick up. The term is there nonetheless, which you will see (I believe) if you solve it with Euler's identity instead of u-substitution.

 

[CAF123]

Which part? I don't understand. I thought that would be enough?

From $e^{iz} = 2\pm \sqrt{3}\Rightarrow iz = \ln (2 \pm \sqrt{3})$, you can expand the RHS, taking into consideration the fact the complex logarithm is multiple valued.

 

[MissP.25_5]

From $e^{iz} = 2\pm \sqrt{3}\Rightarrow iz = \ln (2 \pm \sqrt{3})$, you can expand the RHS, taking into consideration the fact the complex logarithm is multiple valued.

So how should I solve this question? I guess my working is alright up to this part, right?

 

[lurflurf]

in fact by convention the principle value is
$$\mathrm{Cos}^{-1}(2)=\imath\, \mathrm{Cosh}^{-1}(2)=\imath\, \mathrm{Ln}(2+\sqrt{3})$$
to find all solutions recall that
$$\cos(-x)=\cos(x) \\
\text{and for any integer k}\\
\cos(x +2k\, \pi)=\cos(x)$$

 

[CAF123]

So how should I solve this question? I guess my working is alright up to this part, right?

It is, the method is fine. Given $z \in \mathbb{C},$ what is $\log_{e} z$?

 

[MissP.25_5]

in fact by convention the principle value is
$$\mathrm{Cos}^{-1}(2)=\imath\, \mathrm{Cosh}^{-1}(2)=\imath\, \mathrm{Ln}(2+\sqrt{3})$$

I don't get that part. How do you calculate that?

 

[MissP.25_5]

It is, the method is fine. Given $z \in \mathbb{C},$ what is $\log_{e} z$?

$\log_{e} z$ = log_e(x+iy)

Is that correct?

 

[CAF123]

$\log_{e} z$ = log_e(x+iy)

Is that correct?

It is not what I meant for you to write down - have you studied the complex logarithm?

 

[lurflurf]

I don't get that part. How do you calculate that?

Same way you did.

$$\mathrm{Cos}^{-1}(2)=\imath\, \mathrm{Cosh}^{-1}(2)=\imath\, \mathrm{Ln}(2+\sqrt{3})\sim 1.316957896924816708625046347307968444026981971\imath
$$
is the principal value.
That is the agreed reference value we give when we give only one value.
To find all values you do not need to deal with complex logs (though you could).
Just think back to real trigonometry.
We found one value call it P
then -P was another
then we could add 2n ∏

Once we find one solution, we then find them all
what are all solutions to
$$\cos(x)=2$$
is done the same way as
what are all solutions to
$$\cos(x)=0.2$$

 

[MissP.25_5]

It is not what I meant for you to write down - have you studied the complex logarithm?

Yes, I have. But I don't know how to use that here.

 

[MissP.25_5]

Same way you did.

$$\mathrm{Cos}^{-1}(2)=\imath\, \mathrm{Cosh}^{-1}(2)=\imath\, \mathrm{Ln}(2+\sqrt{3})\sim 1.316957896924816708625046347307968444026981971\imath
$$
is the principal value.
That is the agreed reference value we give when we give only one value.
To find all values you do not need to deal with complex logs (though you could).
Just think back to real trigonometry.
We found one value call it P
then -P was another
then we could add 2n ∏

Once we find one solution, we then find them all
what are all solutions to
$$\cos(x)=2$$
is done the same way as
what are all solutions to
$$\cos(x)=0.2$$

Ok, so what do I do next? Am I supposed to expand that log part?

 

[lurflurf]

how would you do the one with 0.2?
It is the same.

If t is any solutions and k is an integer

$$2k\, \pi\pm t$$
is all the solutions because
$$\cos(2k\, \pi\pm t)=\cos(t)$$
by properties of cos(x)

 

[CAF123]

Yes, I have. But I don't know how to use that here.

Ok, so you know that $\log_e z = \text{Log}_e |z| + i\text{Arg}\,z + 2\pi k, \,\,k \in \mathbb{Z}$, where $\log$ is the complex log and $\text{Log}$ is the real log. Use this to obtain the full solution set of the equation $iz = \ln(2\pm \sqrt{3})$.

Alternatively, as lurflurf said, make it clear that you solved for the principal value and, using the properties of the cosine, tag on a $2\pi k.$

 

[MissP.25_5]

how would you do the one with 0.2?
It is the same.

If t is any solutions and k is an integer

$$2k\, \pi\pm t$$
is all the solutions because
$$\cos(2k\, \pi\pm t)=\cos(t)$$
by properties of cos(x)

Are you saying that I have to something like this?

 

[MissP.25_5]

Ok, so you know that $\log_e z = \text{Log}_e |z| + i\text{Arg}\,z + 2\pi k, \,\,k \in \mathbb{Z}$, where $\log$ is the complex log and $\text{Log}$ is the real log. Use this to obtain the full solution set of the equation $iz = \ln(2\pm \sqrt{3})$.

Alternatively, as lurflurf said, make it clear that you solved for the principal value and, using the properties of the cosine, tag on a $2\pi k.$

But how do I find Arg(Z) here? What is the value of r?

 

[MissP.25_5]

Ok, so you know that $\log_e z = \text{Log}_e |z| + i\text{Arg}\,z + 2\pi k, \,\,k \in \mathbb{Z}$, where $\log$ is the complex log and $\text{Log}$ is the real log. Use this to obtain the full solution set of the equation $iz = \ln(2\pm \sqrt{3})$.

Alternatively, as lurflurf said, make it clear that you solved for the principal value and, using the properties of the cosine, tag on a $2\pi k.$

I'm not sure how to plug in the values. But this is my attempt.

 

[lurflurf]

You are over thinking
if we know the solution
$$t=\imath\, \mathrm{Ln}(2+\sqrt{3})$$
to find all solutions we consider the additive inverse and shifts by 2 k pi

$$t=2k\, \pi+\imath\, \mathrm{Ln}(2\pm \sqrt{3})=2k\, \pi\pm\imath\, \mathrm{Ln}(2+ \sqrt{3})$$

 

[MissP.25_5]

You are over thinking
if we know the solution
$$t=\imath\, \mathrm{Ln}(2+\sqrt{3})$$
to find all solutions we consider the additive inverse and shifts by 2 k pi

$$t=2k\, \pi+\imath\, \mathrm{Ln}(2\pm \sqrt{3})=2k\, \pi\pm\imath\, \mathrm{Ln}(2+ \sqrt{3})$$

Wait, so I just have to add 2∏k, right? So that it rotates and rotates and they will return to the same value after each 2∏ rotation, so that will be all the solutions?

Is this right?

 

[lurflurf]

^Yes.
Do you intend you ln to be single valued, or multivalued?

cos has period 2pi so adding an integer multiple of 2pi does not change it

 

[MissP.25_5]

^Yes.
Do you intend you ln to be single valued, or multivalued?

cos has period 2pi so adding an integer multiple of 2pi does not change it

Since the instruction says to find all solutions, doesn't that mean ln have to be multivalued? Multivalued means k>0, right? k=0 would be the principle value, which is single valued, isn't it?
Can you check the attachment?

 

[CAF123]

But how do I find Arg(Z) here? What is the value of r?

$Z_{1,2} = 2 \pm \sqrt{3}$ are both real numbers > 0 so $\text{Arg}\, Z_{1,2} = 0.$

$\log_e z = w \iff z = e^w$, where $\log_e$ on the LHS is the complex logarithm. In your case, $$\log_e e^{iz} = \log_e (2\pm \sqrt{3}) \Rightarrow iz = \dots $$

Expand using the definition of the complex log.

 

[MissP.25_5]

$Z_{1,2} = 2 \pm \sqrt{3}$ are both real numbers > 0 so $\text{Arg}\, Z_{1,2} = 0.$

$\log_e z = w \iff z = e^w$, where $\log_e$ on the LHS is the complex logarithm. In your case, $$\log_e e^{iz} = \log_e (2\pm \sqrt{3}) \Rightarrow iz = \dots $$

Expand using the definition of the complex log.

Have I expanded correctly?
Is that the final answer?

 

[lurflurf]

Since the instruction says to find all solutions, doesn't that mean ln have to be multivalued? Multivalued means k>0, right? k=0 would be the principle value, which is single valued, isn't it?
Can you check the attachment?

That attachment is fine.
It is a minor technicality. To find all solutions we can use a multivalued inverse, or we can use a single value inverse to generate all solutions. k=0 can be the principal value if it is set up that way

your last post is confusing
where did i^0 come from?
third line from the bottom should have 2k pi i
then it should in the next line become 2k pi when you multiply both sides by -i

 

[MissP.25_5]

That attachment is fine.
It is a minor technicality. To find all solutions we can use a multivalued inverse, or we can use a single value inverse to generate all solutions. k=0 can be the principal value if it is set up that way

your last post is confusing
where did i^0 come from?
third line from the bottom should have 2k pi i
then it should in the next line become 2k pi when you multiply both sides by -i

Sorry, it should be i*0, this is due to iargZ. And argZ here is 0.

 

[MissP.25_5]

That attachment is fine.
It is a minor technicality. To find all solutions we can use a multivalued inverse, or we can use a single value inverse to generate all solutions. k=0 can be the principal value if it is set up that way

your last post is confusing
where did i^0 come from?
third line from the bottom should have 2k pi i
then it should in the next line become 2k pi when you multiply both sides by -i

So, is this okay now?

 

[lurflurf]

^Yes that looks good.

 

[MissP.25_5]

^Yes that looks good.

Between the 2 terms, (regarding the final answer) the symbol is just + or is it +/- ? I mean, how to simplify it?