- #1
aaaa202
- 1,169
- 2
I really need help on this question, I've tried asking several people but I still don't quite get it.
The formula for the work done on compressing/expanding an ideal gas is [itex]\int[/itex]-pdV.
Now first of all - p denotes the internal pressure of the gas right?
If so, good so far.
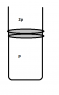
Let us now assume the situation on the picture, where a gas is confined in a cylinder with a movable piston. The gas is not in equilibrium since the external pressure from the atmosphere exceeds the internal (in my example external pressure is twice the internal but it could be anything). Of course the gas will now start to compress.
My question is what the work done on the gas is and why the external pressure for some reason has no influence on the work done.
Let me try to do a force analysis so that you can see what I'm thinking and explain, where I go wrong.
We start noting that the gas will exceed a force on the piston equal to F = Ap, where A is the area of the piston. By Newtons third law the piston then exerts a force of -F on the gas.
Furthermore we see that the external pressure on the piston must exert a force of 2pA and the piston must then exert a force on the atmosphere given by -2pA.
Let's say that the gas piston moves a distance x and for simplicity assume that the pressure stays the same (NOT realistic, I know)
Then it is clear that the work done on the gas in the cylinder is indeed -F*x = -pdeltaV.
*********** BUT SOMETHING IS CLEARLY WRONG. THE PISTON WILL ALSO HAVE GAINED KINETIC ENERGY EQUAL TO THE WORK DONE ON THE GAS! WHERE DOES THIS GO? IT MUST GO TO THE GAS TOO! ***********
I think fundamentally there is something completely wrong with this way of thinking, but I can't understand it in other ways. Please help me understand it such that it makes sense to think of the work done on the gas as just W = -pdeltaV and not twice that work.
The formula for the work done on compressing/expanding an ideal gas is [itex]\int[/itex]-pdV.
Now first of all - p denotes the internal pressure of the gas right?
If so, good so far.
Let us now assume the situation on the picture, where a gas is confined in a cylinder with a movable piston. The gas is not in equilibrium since the external pressure from the atmosphere exceeds the internal (in my example external pressure is twice the internal but it could be anything). Of course the gas will now start to compress.
My question is what the work done on the gas is and why the external pressure for some reason has no influence on the work done.
Let me try to do a force analysis so that you can see what I'm thinking and explain, where I go wrong.
We start noting that the gas will exceed a force on the piston equal to F = Ap, where A is the area of the piston. By Newtons third law the piston then exerts a force of -F on the gas.
Furthermore we see that the external pressure on the piston must exert a force of 2pA and the piston must then exert a force on the atmosphere given by -2pA.
Let's say that the gas piston moves a distance x and for simplicity assume that the pressure stays the same (NOT realistic, I know)
Then it is clear that the work done on the gas in the cylinder is indeed -F*x = -pdeltaV.
*********** BUT SOMETHING IS CLEARLY WRONG. THE PISTON WILL ALSO HAVE GAINED KINETIC ENERGY EQUAL TO THE WORK DONE ON THE GAS! WHERE DOES THIS GO? IT MUST GO TO THE GAS TOO! ***********
I think fundamentally there is something completely wrong with this way of thinking, but I can't understand it in other ways. Please help me understand it such that it makes sense to think of the work done on the gas as just W = -pdeltaV and not twice that work.