- #1
jenny_shoars
- 21
- 0
When given an image of a scene of something like a hallway or road (looking down this hallway or road) a vanishing point can be determined. Also, the points on the image must lie on a certain line in the real world environment given by:
[itex] x_{im} = f\frac{X}{Z} [/itex] and [itex] y_{im} = f\frac{Y}{Z} [/itex]
where [itex]f[/itex] is the focal length of the camera, [itex](x_{im},y_{im})[/itex] is the image point and [itex](X, Y, Z)[/itex] is the world frame point. This is illustrated below.
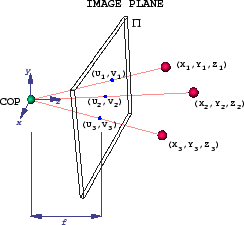
I've found that if the camera optical axis is in the same direction as the hallway/road (i.e. the optical center goes to the vanishing point) and the camera is just a certain height above the ground plane, then it's simple to get the position of a given image point on the ground plane. That being, if [itex]H[/itex] is the height, then:
[itex]Y=-H[/itex], [itex]Z=-H[/itex], [itex]X=-frac{x_{im}H}{y_{im}}[/itex]
This all works fine, but I'm getting a little lost when adding in yaw and pitch to the camera reference frame (no roll). After some work I've found that the ground plane can be represented in the camera reference frame by:
[itex]X sin(\alpha) sin(\beta) + Z sin(\alpha) cos(\beta) + Y cos(\alpha) = H[/itex]
And this is where I'm stuck. I'm not sure how to usefully use the above equation with the first two equations to get [itex]X[/itex], [itex]Y[/itex], and [itex]Z[/itex] from [itex]x_{im}[/itex] and [itex]y_{im}[/itex]. Any suggestions? Thank you much!
[itex] x_{im} = f\frac{X}{Z} [/itex] and [itex] y_{im} = f\frac{Y}{Z} [/itex]
where [itex]f[/itex] is the focal length of the camera, [itex](x_{im},y_{im})[/itex] is the image point and [itex](X, Y, Z)[/itex] is the world frame point. This is illustrated below.
I've found that if the camera optical axis is in the same direction as the hallway/road (i.e. the optical center goes to the vanishing point) and the camera is just a certain height above the ground plane, then it's simple to get the position of a given image point on the ground plane. That being, if [itex]H[/itex] is the height, then:
[itex]Y=-H[/itex], [itex]Z=-H[/itex], [itex]X=-frac{x_{im}H}{y_{im}}[/itex]
This all works fine, but I'm getting a little lost when adding in yaw and pitch to the camera reference frame (no roll). After some work I've found that the ground plane can be represented in the camera reference frame by:
[itex]X sin(\alpha) sin(\beta) + Z sin(\alpha) cos(\beta) + Y cos(\alpha) = H[/itex]
And this is where I'm stuck. I'm not sure how to usefully use the above equation with the first two equations to get [itex]X[/itex], [itex]Y[/itex], and [itex]Z[/itex] from [itex]x_{im}[/itex] and [itex]y_{im}[/itex]. Any suggestions? Thank you much!