- #1
ryho1092
- 3
- 0
Homework Statement
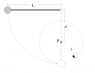
The string in the Figure is L = 113.0 cm long and the distance d to the fixed peg P is 91.5 cm. When the ball is released from rest in the position shown, it will swing along the dashed arc. How fast will it be going when it reaches the lowest point in its swing?
B-How fast will it be going when it reaches the highest point in its swing?
Homework Equations
Conservation on Energy: TE=PE+KE
KE=1/2 mv^2
PE=mgh or mg(L)---L=length of string
The Attempt at a Solution
I got 4.71 m/s for v for the first part. I got this by using conservation of energy, not moving initally and at the bottom (my reference point) no PE.
I'm stuck on the second part. I found my TE by using the starting point, mgh=PE which is 9.8 m/s^2 * 1.13m * m(mass). This should equal my PEtop + KEtop at the top, so
PEtop = mgh=mg(1.13m-.915m) and KEtop should equal 1/m2v^2. Puting it all together I have the following: TE=PE+KE 9.8m/s^2 * 1.13 m * mass = mass * 9.8 m/s^2 * (1.13-.915)m + 1/2 * mass * v^2. The masses cancle out, and I solve for v= SQRT(2*(9.8*1.13-9.8*1.13-91.5))= 4.23 m/s
But this isn't accepted by capa, what did I do wrong? Thanks in advance
Ryan
Attachments
Last edited: