- #1
ttttrigg3r
- 49
- 0
Hello. I've uploaded the question onto pictures and linked them. I hope this method of asking a question works.
I'm trying to find the mass of the ball, but I get the square root of a negative number. Can someone take a look to see if I'm doing this problem correctly?

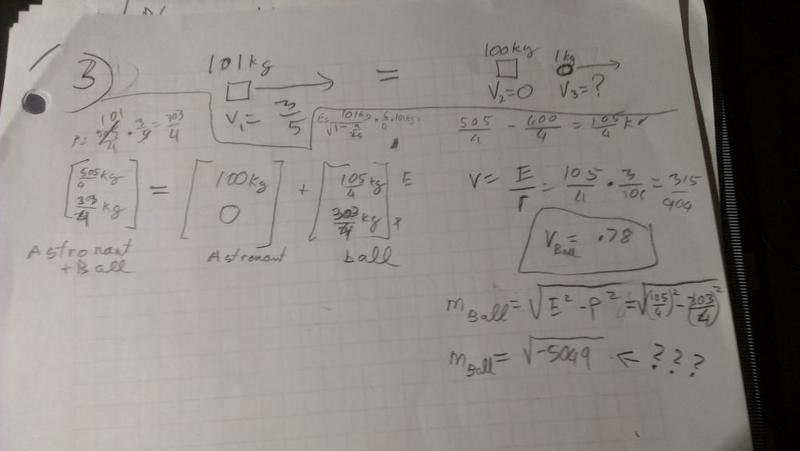
I'm trying to find the mass of the ball, but I get the square root of a negative number. Can someone take a look to see if I'm doing this problem correctly?