- #1
ritwik06
- 580
- 0
Homework Statement
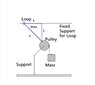
http://img510.imageshack.us/img510/5505/systemet4.jpg
What I wish to do is to relate the accelerations of the loop an the massive block. I know the angle theta at any instant. I also know that the acceleration of the loop on the fixed support is a. I have been given no other information except the figure and I have to write out the acceleration of the block.
My teacher says its a cos theta
But I cannot express the expression of the block in just two variable of a and theta. I also need the perpendicular distance of the fixed support from the pulley.
please help me!
Last edited by a moderator: