- #1
Michael_Light
- 113
- 0
Homework Statement
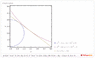
2 circles have the equation x2+y2-2x-2y+1=0 and x2+y2-12x-12y+36=0 respectively. Both circle touches the x-axis, y-axis and the line 3x + 4y = 12. Find the fourth tangent of the 2 circles.
Homework Equations
The Attempt at a Solution
This is second part of the question, I solved the first part which require to find the equation of the 2 circles... And now i stuck at this final part... can anyone help me?