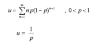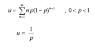Could you help me with a proof geometric progression

[Gunmo]

My Statistics textbook does not prove this. The author think it is commons sense. I am not sure about this proof.

Thank you.

 

[Mark44]

Below is the contents of your attachment.
$$u = \sum_{n = 1}^\infty x p(1 - p)^{n - 1}$$
$$ u = \frac 1 p$$
I would not consider this a proof in any way, in part because neither x nor p is defined.

 

[Gunmo]

sorry typo, i attach again

 

[Gunmo]

Could you have a look new attachment please.
Thank you for finding error in attachment

 

[PeroK]

Could you have a look new attachment please.
Thank you for finding error in attachment

Do you know the Binomial Theorem?

 

[Gunmo]

Yes, this is actually about probability.

 

[PeroK]

Yes, this is actually about probability.

The proof you are looking for involves the Binomial Theorem - which, given you are dealing with a Binomial Distribution, may not be that surprising.

Hint: take out the factor of $p$ and deduce from the answer what the remaining infinite sum must be. Then try to find the trick.

 

[Gunmo]

Not sure yet, this eventually

Sigma ( x * k^x) 0<k<1 x = 1, 2, 3, 4, 5....n=infinite

x is approach infinite,
k^x approach 0.

The answer is, 1/k.

 

[PeroK]

Not sure yet, this eventually

Sigma ( x * k^x) 0<k<1 x = 1, 2, 3, 4, 5....n=infinite

x is approach infinite,
k^x approach 0.

The answer is, 1/k.

I'm not sure what that all means. Here's some latex. If you reply to my post, you'll get the Latex:

$$\sum_{n=1}^{\infty} np(1-p)^{n-1} = \frac{1}{p}$$

 

[Charles Link]

Instead of being a binomial distribution (it doesn't have the combinations term), it looks like it is computing the mean number of times you need to flip a (weighted)coin before it comes up heads, with "p" being the probability that heads comes up on any given throw. @PeroK gives a good hint: You need to look for a "trick" of solving the summation of $n(1-p)^{n-1}$. I can add to that: the trick involves taking a derivative. $\\$ Editing: The OP @Gunmo mentions in the original post, that the author says this is a "common sense" result. It's good to prove it mathematically, but it does make sense in that if you have a probability $p=\frac{1}{100}$ for a success, in general you need approximately $\bar{n}= \frac{1}{p}=100$ tries to get a success.

 

[StoneTemplePython]

There are a lot of ways to solve this problem...

As mentioned, you are trying to find the expected value associated with a geometric distribution here. The solutions mentioned thus far do not address convergence issues. So long as you are ok with that / understand the radius of convergence of a geometric series, I would suggest using the memoryless property of a geometric distribution.

That is: you are calculating expected number of coin flips until heads, where heads occurs with probability $p$. Your expected value calculation is: you have one coin toss no matter what, and then with probability $1 - p$ you get a tails and thus are starting over with the exact same incremental expectation -- again because of memorylessness

$E[X] = 1 + (1-p)E[X]$

Then solve for $E[X]$

If you are worried about convergence you either need to explicitly address radius of convergence or set this up as an absorbing state markov chain (2 states only), and use telescoping on the partitioned matrix. In the the latter case, convergence is not an issue that needs addressed. Markov chains are overkill here, but I do like the pictures associated with them, and they provide a nice alternative approach when dealing with convergence questions.

 

[PeroK]

$E[X] = 1 + (1-p)E[X]$

Then solve for $E[X]$

.

That's neat.

There are no convergence issues to worry about if you apply the binomial theorem.

 

[Charles Link]

@PeroK : Please read my post #10. I don't think it is binomial. As @StoneTemplePython says, here the OP's problem is to calculate the expected number of coin flips until heads occurs, given that heads occurs with probability p. (The OP's formula is not calculating the probability of $k$ successes in $n$ trials, nor the mean number of successes of a binomial distribution.) $\\$ Note: The "trick" that is most readily employed in solving this one is essentially the same one (taking a derivative w.r.t. $p$) in solving the mean $k$ for a binomial, but this one is not the binomial distribution.

 

[PeroK]

@PeroK : Please read my post #10. I don't think it is binomial. As @StoneTemplePython says, here the OP's problem is to calculate the expected number of coin flips until heads occurs, given that heads occurs with probability p. (The OP's formula is not calculating the probability of $k$ successes in $n$ trials, nor the mean number of successes of a binomial distribution.) $\\$ Note: The "trick" that is most readily employed in solving this one is essentially the same one (taking a derivative w.r.t. $p$) in solving the mean $k$ for a binomial, but this one is not the binomial distribution.

If this isn't a binomial distribution I don't know what is. True, you are calculating the mean time to get the first occurrence, but it's clearly a binomial.

 

[PeroK]

If this isn't a binomial distribution I don't know what is. True, you are calculating the mean time to get the first occurrence, but it's clearly a binomial.

Actually, this isn't quite right. It's a Bernoulli Process, the Binomial distribution being a number of Bernoulli trials. I've always used Binomial for both cases, where there are only two outcomes.

The binomial theorem applies in any case.

 

[Gunmo]

This mean of geometric probability problem.
No statistics and Math textbook proved it. I proved it now.
.