What are the properties and equations of a 4-dimensional cube?

[DaMeekie]

We all have a pretty good understanding about our three dimensions.

First starting off with 0D or a point in space = 360º. Then 1D being a line = 180º. Moving to 2D such as a square = 90º. Finally ending with 3D = 45º. It is important to state that finding these angles requires the viewer to be looking from a perfect bird's eye view to the center of each dimension.

An interesting yet very simple pattern emerges while doing this being the next dimension in this infinite series is just 1/2 the last.

With this statement we can easily find what 4D square angle would be from a perfect bird's eye view which would be 45º/2 = 22.5º.

Drawing a 4 dimensional square is a little tricky but I've managed to map one out.

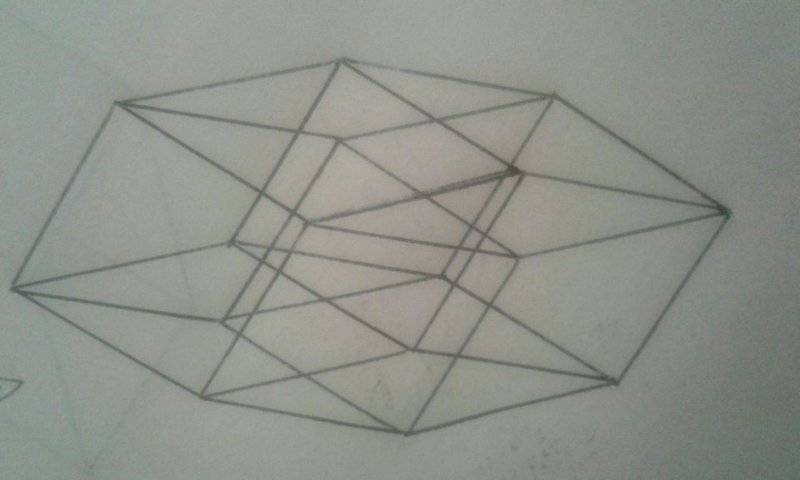
I don't particularly know any use or further meaning this might hold, but any information would be wonderful.

 

[mfb]

Finally ending with 3D = 45º

45º where?

There is no proper view on a cube where 45º angles would be special in any way. The simple cube sketches on paper do not represent a possible 3D view.

 

[DaMeekie]

45º where?

There is no proper view on a cube where 45º angles would be special in any way. The simple cube sketches on paper do not represent a possible 3D view.

 

[DaMeekie]

View attachment 112939

To note when I say a perfect bird's eye view. Which is looking directly at the focal center from a perpendicular angle. Any three dimensional crystal lattice with a perfect shape such as a cube or a sphere would appear the same in both 2 and 3 dimension

 

[mfb]

The simple cube sketches on paper do not represent a possible 3D view.

See above.

Yes it is often drawn like you did, but that is not an accurate picture. No bird can ever see a cube that way. If you see the third dimension the front cannot have 90 degree angles, which also means you cannot have two 45 degree angles there. You can have one - but that is pure coincidence then.

 

[DaMeekie]

If you see the third dimension the front cannot have 90 degree angles

I need further iteration for that to make any sense. I hope you also realize that this isn't a solid surface this is just lines and points. Just like a lattice structure.

It is possible to model a 3 dimensional space on 2 dimensions. With proper angles and lengths to keep congruencies. I see 3D moving models on my 2D monitor screen pretty regularly. I do not think it is intelligent to disregard those models just because they are 2D virtual. The same goes with my virtual model, it keeps perfect lengths and angles. True it is not real, but I need something more if you want to convince me that I am wrong.

 

[mfb]

If you look at a square in 3 dimensions, you only see it as a square (4 sides of equal length at 90 degree angles) if your point of view is along the axis going through the center of that square. But then your view of a cube doesn't look like you drew it. If you take a point of view where the cube looks roughly like you have shown it, then the angles are 90 degrees any more. You get a parallelogram. In the extreme case, it looks like this.

 

[DaMeekie]

So you say because a cube such as this one does not actually have 90º because it is on 2d paper?

True if you figured the actual angle is truly 120º which is not = 90º.

However when you draw out the other three lines to finish the cube as if there were no surfaces it would look like this.

Yet again the adjacent lines connecting the back of the cube cut the front cubes in half. Into 60º angles.

Now though the virtual angles on the 2d cube were 120º, but the real angles still are represented as 90º. The lines that move through the 3d space seen to cut through to the center and look to be at 60º in 2d.

Granted I didn't generate the cube properly and I can work on doing so I still believe you can accomplish the same result just half the 60 and go from there I'll respond with what one looks like soon enough to verify or falsify my hypothesis. Thank you for your insight

 

[Philip]

I'm not sure why you go from a 180° for a 1D line, to a 90° angle within a 2D square, to 45° for a cube.

For n-dimensional cubes, all 1D edges meet at the vertices, at 90° angles of each other.

The 1D line has only one edge and two vertices, so there are no angles between anything, because there is only 'one thing'. The space above and below the line do not count, since that is the 2nd dimension, and we're not supposed to be using it to measure angles yet, because we're still in the 1st dimension.

A 2D square has 4 corners where 2 lines meet, all at 90 degrees of each other

A 3D cube has 8 corners where 3 lines meet, all at 90 degrees of each other (look at the ceiling corner in your house/apartment, there's 3 lines converging)

A 4D tesseract has 16 corners where 4 lines meet, all at 90 degrees of each other

A 5D penteract has 32 corners where 5 lines meet, all at 90 degrees of each other

A 6D cube (hexeract) has 64 corners where 6 lines meet, all at 90 degrees of each other

An nD cube has 2ⁿ corners where n lines meet, all at 90 degrees of each other

Your drawings are of 3D and 4D cubes, but you had to flatten them onto a 2D sheet of paper. Well, that messes with the appearance of the angles. A 2D drawing of a 3D cube will not directly show you the perfect 90° angles that it really has, right? And, trying to flatten the already flattened 3D shadow of a 4D cube onto paper will cause even more distortion of apparent angles.

 

[DaMeekie]

In response to Philip

A straight line in a 2+ dimensional plane is an angle it's at 180º
The 90º In a square is obvious
The 45º (technically 60º from 2d standpoint) angle shows when you superimpose the back parimeter into the foreground. This is a somewhat constant when looking at the cube from a specific view point so you can make further assumptions as long as the formula States true.

Yes every angle in any further dimension will actually be 90º but that does not mean that they appear that way in smaller dimensions because of spatial warping. The lines and angles would be in very specific points due to the nature of the mathematics placed behind this and an intelligent mind should be able to formulate where those lines and angles would be. That is exactly what I'm trying to toy with to see further than what we actually think we know.

 

[Philip]

A straight line in a 2+ dimensional plane is an angle it's at 180º

With respect to what, though? That's like saying a cube in 4D space is 180°. What exactly are you measuring?

The 45º (technically 60º from 2d standpoint) angle shows when you superimpose the back parimeter into the foreground. This is a somewhat constant when looking at the cube from a specific view point so you can make further assumptions as long as the formula States true.

Where are you getting the 45° from? Can you share this formula with us? How can it be 60° in 2D?

Yes every angle in any further dimension will actually be 90º but that does not mean that they appear that way in smaller dimensions because of spatial warping.

It's not a spatial warping, that deals with non-euclidean (hyperbolic, spherical) spaces. What you meant was perspective projection.

The lines and angles would be in very specific points due to the nature of the mathematics placed behind this and an intelligent mind should be able to formulate where those lines and angles would be.

Yes, this is correct. But, it's not that difficult to define the 16 vertices of a 4D cube in R⁴, which is (±1, ±1, ±1, ±1), and project them onto a 3-plane, then display it on your 2D monitor. Someone already did that here:

That is exactly what I'm trying to toy with to see further than what we actually think we know.

What more is there to know about the n-cube series? The mathematics is rather simple, and well understood. We even know some of the more bizarre properties of +100D cubes, and how they differ to a 3D/4D/5D "normal" cube.

So, as stated before, an n-dimensional cube has 2ⁿ corners (vertices) while only 2n faces (which are n-1D cubes). And, we find that we get a very disproportionate number of pointy corners to flat faces. A 100D cube is almost entirely made out of its corners, and thus most of its volume is concentrated there. That's 1.2676506 * 10³⁰ corners compared to 200 faces (99D cubes)

The distance you must travel from corner to corner is far greater than from mid-face to mid-face. If you picked up a 100D cube, you would feel most of its mass in the corners, with a mostly empty-feeling center, however that would really feel.

Also, the elements (0D corners, 1D edges, 2D faces, 3D cells, etc) can be derived with the simple formula (x+2)ⁿ , where n = dimensions of the cube. Expanding this into a polynomial, you will find that the coefficients of xⁿ are the number of elements, per dimension n .

We can even define the surface of n-cubes with an implicit equation, which goes like:

• 1D Line :

|x| = a• 2D square :

|x-y| + |x+y| = a• 3D cube :

||x-y|+|x+y| -2z| + ||x-y|+|x+y| +2z| = a• 4D cube :

||x-y|+|x+y| - |z-w|-|z+w|| + ||x-y|+|x+y| + |z-w|+|z+w|| = a• 5D cube :

|||x-y|+|x+y| -2z| + ||x-y|+|x+y| +2z| - 2|w-v|-2|w+v|| + |||x-y|+|x+y| -2z| + ||x-y|+|x+y| +2z| + 2|w-v|+2|w+v|| = a