- #1
phazei
- 9
- 0
In this problem, you will estimate the cross section for an earth-asteroid collision. In all that follows, assume that the Earth is fixed in space and that the radius of the asteroid is much less than the radius R of the earth. The mass of the Earth is M_e, and the mass of the asteroid is m. Use G for the universal gravitational constant. View Figure
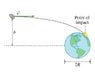
There is a height b that can be seen in this picture:
http://phazei.8m.com/ext/phys.jpg
For large earth-asteroid separation, what is the magnitude of the asteroid's total angular momentum L_initial about the center of the earth?
L_initial =m*b*v
The maximum impact parameter for which collision is guaranteed, b=b_{\rm max}, is obtained by setting the minimum earth-asteroid separation equal to the radius R of the earth. This is the configuration shown in the figure. In this case, it is clear that the velocity of the asteroid right before it hits the Earth is tangent to the surface and therefore perpendicular to the position vector that points from the center of the Earth to the asteroid.
When b=b_max, what is the total energy E_surface of the asteroid the instant before it crashes into the earth? Assume that the speed of the asteroid at closest approach is v_f.
E_surface =(1/2)*m*v_f^2-G*m*M_e/R
Again, suppose that b=b_max. What is the angular momentum L_surface of the asteroid the moment before it crashes into the Earth's surface?
Express your answer in terms of m, M_e, R, v_f, and G.
L_surface =m*R*v_f
I was able to get all the with a bit of work, but this next part I am stumped on.
Use conservation of energy and angular momentum to find an expression for (b_max)^2.
I found m*b_max*v=m*R*v_f, I solved for v_f and put it into the E_surface equation and solved for b_max^2= 2*G*M_e*R/v^2
but apparently that's wrong :(
What's wrong with it?
Then it asks
The collision cross section S represents the effective target area "seen" by the asteroid and is found by multiplying (b_max)^2 by pi. If the asteroid comes into this area, it is guaranteed to collide with the earth.
A simple representation of the cross section is obtained when we write v in terms of v_e, the escape speed from the surface of the earth. First, find an expression for v_e, and let v=Cv_e, where C is a constant of proportionality. Then combine this with your result for (b_max)^2 to write a simple-looking expression for S in terms of R and C.
But I need the previous part to do that...
There is a height b that can be seen in this picture:
http://phazei.8m.com/ext/phys.jpg
For large earth-asteroid separation, what is the magnitude of the asteroid's total angular momentum L_initial about the center of the earth?
L_initial =m*b*v
The maximum impact parameter for which collision is guaranteed, b=b_{\rm max}, is obtained by setting the minimum earth-asteroid separation equal to the radius R of the earth. This is the configuration shown in the figure. In this case, it is clear that the velocity of the asteroid right before it hits the Earth is tangent to the surface and therefore perpendicular to the position vector that points from the center of the Earth to the asteroid.
When b=b_max, what is the total energy E_surface of the asteroid the instant before it crashes into the earth? Assume that the speed of the asteroid at closest approach is v_f.
E_surface =(1/2)*m*v_f^2-G*m*M_e/R
Again, suppose that b=b_max. What is the angular momentum L_surface of the asteroid the moment before it crashes into the Earth's surface?
Express your answer in terms of m, M_e, R, v_f, and G.
L_surface =m*R*v_f
I was able to get all the with a bit of work, but this next part I am stumped on.
Use conservation of energy and angular momentum to find an expression for (b_max)^2.
I found m*b_max*v=m*R*v_f, I solved for v_f and put it into the E_surface equation and solved for b_max^2= 2*G*M_e*R/v^2
but apparently that's wrong :(
What's wrong with it?
Then it asks
The collision cross section S represents the effective target area "seen" by the asteroid and is found by multiplying (b_max)^2 by pi. If the asteroid comes into this area, it is guaranteed to collide with the earth.
A simple representation of the cross section is obtained when we write v in terms of v_e, the escape speed from the surface of the earth. First, find an expression for v_e, and let v=Cv_e, where C is a constant of proportionality. Then combine this with your result for (b_max)^2 to write a simple-looking expression for S in terms of R and C.
But I need the previous part to do that...
Attachments
Last edited by a moderator: