- #1
hover
- 343
- 0
Homework Statement
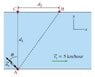
A swimmer wants to cross a river, from point A to point B, as shown in the figure. The distance d_1 (from A to C) is 200m , the distance d_2 (from C to B) is 150m, and the speed v_r of the current in the river is 5 km/h. Suppose that the swimmer's velocity relative to the water makes an angle of [tex]\theta = 45 degrees[/tex] with the line from A to C, as indicated in the figure.
To swim directly from A to B, what speed u_s, relative to the water, should the swimmer have?
Homework Equations
I would think that you would use nothing more than some trig, Pythagorean theorem and stuff about adding and subtracting vectors
The Attempt at a Solution
I have no idea how to attempt this solution. I don't know where to even start. I know the answer is 4.04km/h but I have no idea how to get to that answer. Where should I start?