Current through ring in solenoid-ring system

[lorenz0]

Homework Statement

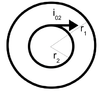
A superconducting solenoid of length $l$, which we can nonetheless asumme as of infinite length has radius $r_1,\ n\ \text{turns}/m$ and is coaxial with a metallic ring of radius $r_2<r_1$, of trascurable self-inductance and resistance $R$. The current through the solenoid and the ring at $t=0s$ is, respectively, $i_{01}=0\ A$ and $i_{02}>0$ in the direction shown in the figure.
Find:

(a) Inductance of the solenoid and the coefficient of mutual inductance between the solenoid and the ring;

(b) The electric current going around the ring at $t_0>0$;

(c) The total magnetic field at the center of the ring at time $t_0$;

(d) The magnetic energy of the solenoid at time $t_0$:

(e) The electric charge which has gone around the ring between times $t=0$ and $t_0$.

Relevant Equations

$\phi=LI;\ \mathcal{E}_2=-\frac{d\phi_2}{dt}=-M\frac{dI_1}{dt}; M_{21}=M_{12}.$

The following is my solution to this problem; I would appreciate some feedback, especially on part (b), which I have found the most challenging. Thanks.

(a) Using Ampere's Law I get $B=\mu_0 n i_1$ where $i_1$ is the current through the solenoid, and since $\phi=Li_1$, where $L$ is the self-inductance, it follows that $L=\pi r_1^2 n^2 \mu_0 l$.
For the mutual inductance, since $M_{12}=M_{21}=M$ we can consider the situation where the current $i$ is flowing through the solenoid giving a magnetic flux through the ring $\phi=B_1 \pi r_2^2=\mu_0 ni\pi r_2^2=M i$ so $M=\mu_0n\pi r_2^2$.

(b) From Faraday's Law we have that $\mathcal{E}_1=-M\frac{di_2}{dt}-L\frac{di_1}{dt}$ (1) and $\mathcal{E}_2=-M\frac{di_1}{dt}$ (2). From (1) we get $i_1 R_{sol}=M\frac{di_2}{dt}-L\frac{di_1}{dt}$ which implies (since $R_{sol}=0$, the solenoid being superconducting) $0=M\frac{di_2}{dt}-L\frac{di_1}{dt}$ so $\frac{di_1}{dt}=-\frac{M}{L}\frac{di_2}{dt}$ which, substituted in (2) gives: $\mathcal{E}_2=-M\left( -\frac{M}{L}\frac{di_2}{dt} \right) \Rightarrow i_2 R=\frac{M^2}{L}\frac{di_2}{dt}\Rightarrow \frac{LR}{M^2}dt=\frac{di_2}{i_2}\Rightarrow \int_{t=0}^{t=t_0}\frac{LR}{M^2}d\bar{t}=\int_{i_2(0)}^{i_2(t_0)}\frac{d\bar{i_2}}{\bar{i_2}}\Rightarrow i_2(t_0)=i_2(0)e^{\frac{LR}{M^2}t_0}$

(c) $\vec{B}=\left(\frac{\mu_0 i_2(t_0)}{2r_2} + \mu_0 ni_1(t_0)\right)\hat{k}$ where the first term is the magnetic field at the center of the ring due to the current through the ring which I got using Biot-Savart's law; also, we can get $i_1(t_0)$ from (b)(1) since $\frac{di_1}{dt}=-\frac{M}{L}\frac{di_2}{dt}=-\frac{M}{L}i_2(0)\frac{LR}{M^2}e^{\frac{LR}{M^2}t}=-\frac{i_2(0)R}{M}e^{\frac{LR}{M^2}t}\Rightarrow i_1(t_0)=-\frac{i_2(0)M}{L}e^{\frac{LR}{M^2}t_0}$

(d) $U(t_0)=\frac{1}{2}Li_1^2(t_0)$

(e) $q_2(t_0)=\int_{0}^{t_0}i_2(t) dt$

 

[anathema]

Overall, your solution seems to be correct and well-thought-out. Here are a few suggestions for improvement:

(a) You could provide a bit more explanation for the steps you took to arrive at the final expressions for L and M. This will make it easier for readers to follow your thought process and understand the equations.

(b) Your solution for part (b) is correct, but it would be helpful to provide a bit more explanation for the steps you took. For example, you could explain why you set the solenoid resistance to zero, and why you substituted your expression for di1/dt into equation (2). This will make it easier for readers to understand your reasoning and follow the calculations.

(c) In part (c), it would be helpful to provide a brief explanation of how you used Biot-Savart's law to calculate the magnetic field at the center of the ring. This will make it easier for readers to understand your approach and the final expression for B.

(d) Your solution for part (d) is correct, but it would be helpful to provide a bit more explanation for the steps you took. For example, you could explain why you used the expression for i1(t0) from part (b) to calculate the energy.

(e) Similarly, in part (e), you could provide a brief explanation of why you integrated the expression for i2(t) over time to calculate the charge on the ring.

In summary, your solution is correct and well-written, but providing a bit more explanation and context for your calculations will make it easier for readers to understand your approach and follow your calculations.