- #1
FS98
- 105
- 4
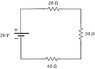
in a circuit like the one in the attached picture, the voltage between two points in between two resistors should be 0.
But there is current flowing through the circuit.
So what’s going on here? Does ohms law not apply in this situation for some reason?
But there is current flowing through the circuit.
So what’s going on here? Does ohms law not apply in this situation for some reason?