Curvature Numerical Gauss etc.

[Omega0]

Hi!

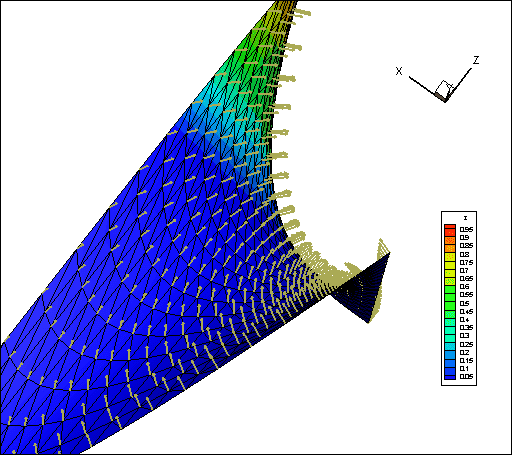
I would like to calculate the curvature for a surface S:R^2->R'3 numerically.
The problem: I simply have the surface as a mesh like you see in the image attached.

I calculated the linearly interpolated face normals in the nodes, too. You see the vectors.

Question: How would you calculate the Gauss curvature from this information?

Thanks!

Best wishes,
Jens

 

[andrewkirk]

Since each node is at the centre of a hexagon, and surrounded by six other equally close nodes, I suggest you calculate the curvature along each of the six lines running through each point, using the line segments connecting the centre point to each of the two points either side of it along every given line. THen multiply the maximum out of the six by the minimum. It's fairly crude, but may be good enough, and I can't easily think of a better method.

 

[mathwonk]

do you mean the total (integral of the ) gauss curvature? or the curvature at some point. technically gauss curvature is taken separately at each point.