- #1
JD96
- 33
- 0
Hello,
I got interested in the concept of rapidity and would like to know a bit more about it. Unfortunately hyperbolic trigonometric functions are not taught in school, at least not where I'm living, so despite the fact that they preserve many characteristics of ordinary trigonometric functions I don't know why they are defined the way they are.
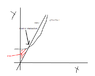
I know that rapidity can be defined as the arclength of the unit hyperbola or as an hyperbolic angle (and probably many more ways). The latter is expressed as Φ= tanh-1(v/c). I searched for definitions of hyperbolic angles that look like this, but couldn't find one. So I tried to make sense of it using an analogy of "normal" angles: In a cartesian coordinate system S the angle between the y-axis and the y-axis of another coordinate system S', that has been rotated in negative x-direction, is given by α= tan-1(1/m) , where m is the slope of y'. Am I correct that the same holds true for the hyperbolic angle between the ct-, and ct'-axis, namely that Φ= tanh-1(1/m) and since 1/m = v/c one gets the definition of rapidity I wrote above?
Thanks in advance!
I got interested in the concept of rapidity and would like to know a bit more about it. Unfortunately hyperbolic trigonometric functions are not taught in school, at least not where I'm living, so despite the fact that they preserve many characteristics of ordinary trigonometric functions I don't know why they are defined the way they are.
I know that rapidity can be defined as the arclength of the unit hyperbola or as an hyperbolic angle (and probably many more ways). The latter is expressed as Φ= tanh-1(v/c). I searched for definitions of hyperbolic angles that look like this, but couldn't find one. So I tried to make sense of it using an analogy of "normal" angles: In a cartesian coordinate system S the angle between the y-axis and the y-axis of another coordinate system S', that has been rotated in negative x-direction, is given by α= tan-1(1/m) , where m is the slope of y'. Am I correct that the same holds true for the hyperbolic angle between the ct-, and ct'-axis, namely that Φ= tanh-1(1/m) and since 1/m = v/c one gets the definition of rapidity I wrote above?
Thanks in advance!
Last edited: