- #1
Rex Galilae
- 1
- 0
I went through my Physics textbook where we have a chapter on Communication systems. There's a certain section where they show us the formula for the LOS max. range for a tower with a given height (say h) but I, unsatisfied with it, set out to derive it myself at home and wasn't convinced with the results.
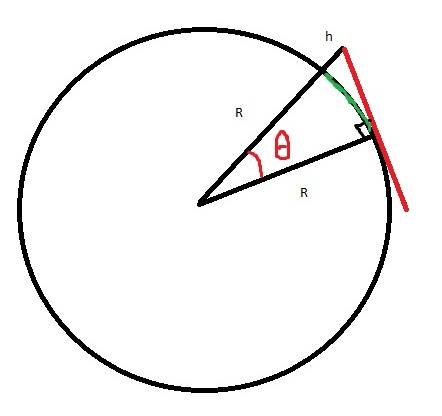
First off, I assumed that the max. LOS range can be thought of as the length of the arc subtended by the tower and the point of max range at the center of the Earth. If we draw a line from the top of the tower to the max. range point, it hits the surface of Earth tangentially.
Connect the base of the tower and the max. range point to the center of the Earth and we get a right triangle (since the line is tangential to the surface of Earth). Using trigonometry, we find out that the angle subtended at the center (θ) by these two points (green) can be expressed as cos-1(R/R+h) where R is the Radius of the Earth.
Now that we have the angle, it's easy to calculate the length of the arc (i.e. the distance b/w the tower and the point of max. range) by using this simple formula which is l = R*θ.
This gives us that l = R*cos-1(R/R+h).
(You can use the small angle approximation to refine the formula a bit)
But then, when I used this formula to calculate LOS max. range problems from the book, my answers were a long way off their values. I'm doubting that something is wrong with my first assumption. Pls. help!
First off, I assumed that the max. LOS range can be thought of as the length of the arc subtended by the tower and the point of max range at the center of the Earth. If we draw a line from the top of the tower to the max. range point, it hits the surface of Earth tangentially.
Connect the base of the tower and the max. range point to the center of the Earth and we get a right triangle (since the line is tangential to the surface of Earth). Using trigonometry, we find out that the angle subtended at the center (θ) by these two points (green) can be expressed as cos-1(R/R+h) where R is the Radius of the Earth.
Now that we have the angle, it's easy to calculate the length of the arc (i.e. the distance b/w the tower and the point of max. range) by using this simple formula which is l = R*θ.
This gives us that l = R*cos-1(R/R+h).
(You can use the small angle approximation to refine the formula a bit)
But then, when I used this formula to calculate LOS max. range problems from the book, my answers were a long way off their values. I'm doubting that something is wrong with my first assumption. Pls. help!