- #1
Clever Penguin
- 74
- 20
I was bored, so I decided to derive the special relativity formulae.
I drew the following diagram of a light clock:
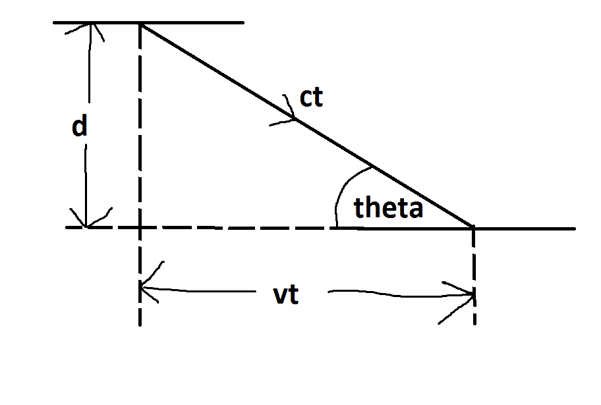
In order to find t, I did sinθ=d/ct
Which gives tsinθ=d/c
Which gives t=d/csinθ
If v = 0, vt = 0, and θ = 90
sin90 = 1
t = d/csinθ = d/c
We call this t0If v is greater than 0, vt is greater than zero, and θ is less than 90
sin90 is less than1
t = d/csinθ is greater than d/c
We use Pythagoras to get t0=t(1- (v2/c2))-1/2
What are the steps involved in getting to this answer?
I drew the following diagram of a light clock:
In order to find t, I did sinθ=d/ct
Which gives tsinθ=d/c
Which gives t=d/csinθ
If v = 0, vt = 0, and θ = 90
sin90 = 1
t = d/csinθ = d/c
We call this t0If v is greater than 0, vt is greater than zero, and θ is less than 90
sin90 is less than1
t = d/csinθ is greater than d/c
We use Pythagoras to get t0=t(1- (v2/c2))-1/2
What are the steps involved in getting to this answer?