- #1
mk9898
- 109
- 9
How/why does the first equal sign hold? Where does each derivative come from:
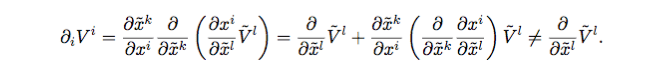
That is the second term, not the first term...mk9898 said:
A tensor is a mathematical object that represents a physical quantity with multiple components, each of which can vary in different directions. It is important in science because it allows us to describe and analyze complex systems with multiple variables, such as fluid dynamics, electromagnetism, and general relativity.
The derivative of a tensor is calculated using the same rules as the derivative of a scalar. However, since a tensor has multiple components, the derivative will also have multiple components, resulting in a tensor of a higher rank. This can be done using the chain rule and the product rule, as well as the rules for differentiating trigonometric and exponential functions.
The concept of a tensor was first introduced by mathematician Gregorio Ricci-Curbastro in the late 19th century as a way to generalize the concept of a vector. It was further developed by mathematician Tullio Levi-Civita and physicist Albert Einstein in the early 20th century as a key tool in their formulation of the theory of general relativity.
A tensor can be represented mathematically as a multi-dimensional array of numbers, with each number representing a component of the tensor in a specific direction. The number of indices in the array corresponds to the rank of the tensor, and the dimensions of the array correspond to the number of components in each direction.
Tensors have many real-world applications in various fields of science and engineering. In physics, they are used to describe the stress and strain of materials, as well as the curvature of space-time in general relativity. In engineering, they are used in the design of structures and machines, as well as in computer vision and image processing. They are also used in machine learning and data analysis, such as in the field of deep learning for image and speech recognition.