Deriving Feynman rules out of a generating functional

[JD_PM]

Homework Statement

Given the generating functional (repeated indices in the same term are assumed to be summed over)



\begin{equation}
Z[w] := \frac{1}{(2 \pi)^{n/2}} \int d^n x \prod_{i=1}^n d \bar{\theta}_i d \theta_i \exp \left( -\bar{\theta}_i \partial_j w_i (x) \theta_j - \frac 1 2 w_i (x) w_i (x) \right) \tag{1}
\end{equation}



We define



\begin{equation*}
w_i(x) := x_i + \frac 1 2 g_{ijk} x_j x_k, \quad \text{where} \quad g_{ijk} = g_{ikj} = g_{kij}
\end{equation*}



Where $g_{ijk}$ is assumed to be small.



a) Find the Feynman rules.



b) Find the one- and two-loop contributions to $Z[g]$

Relevant Equations

N/A

To approach the problem I first studied section 1.3 and, more importantly, 1.4 of Osborn's notes.

We first need to compute $\partial_j \omega_i (x)$ and $\omega_i (x)\omega_i (x)$

\begin{equation*}
\partial_j \omega_i (x) = \delta_{ij} + \underbrace{\partial_j (g_{ilm})}_{=0}x_l x_m + g_{ijk}x_k
\end{equation*}

\begin{align*}
\omega_i \omega_i &= \left( x_i + \frac 1 2 g_{ijk} x_j x_k\right) \left(x_i + \frac 1 2 g_{ilm} x_l x_m \right) \\
&= x_i x_i + \frac 1 4 g_{ijk} g_{ilm} x_j x_k x_l x_m + g_{ijk}x_i x_j x_k
\end{align*}

Plugging the given definition of $\omega_i (x)$ into $(1)$ yields

\begin{align*}
Z[w] &= \frac{1}{(2 \pi)^{n/2}} \int d^n x \prod_{i=1}^n d \bar{\theta}_i d \theta_i \exp \left( -\bar{\theta}_i \partial_j w_i (x) \theta_j - \frac 1 2 w_i (x) w_i (x) \right) \\
&= \frac{1}{(2 \pi)^{n/2}} \int d^n x \prod_{i=1}^n d \bar{\theta}_i d \theta_i \exp \Big( -\bar{\theta}_i \delta_{ij} \theta_j - g_{ijk} \bar{\theta}_i \theta_j x_k \\
&- \frac 1 2 x_i x_i -\frac 1 2 g_{ijk} x_j x_k - \frac 1 8 g_{ijk} g_{ilm} x_j x_k x_l x_m \Big) \\
&= \int \prod_{i=1}^n d \bar{\theta}_i d \theta_i \exp(-\bar{\theta}_i \delta_{ij} \theta_j ) \frac{1}{(2 \pi)^{n/2}} \int d^n x \exp\Big( -\frac 1 2 \vec x \cdot \vec x \\
&+ \vec b \cdot \vec x - V(x) \Big)
\end{align*}

Where

\begin{equation*}
b_k := g_{ijk} \theta_i \bar{\theta}_j, \quad \text{noticing} \quad \{ \theta, \bar{\theta}\} = 0
\end{equation*}

\begin{equation*}
V(x) = + \frac 1 2 g_{ijk} x_j x_k + \frac 1 8 g_{ijk} g_{ilm} x_j x_k x_l x_m
\end{equation*}

Next we work out the potential. Based on Osborn's (1.132)

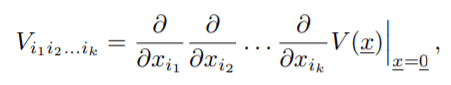
I get

\begin{equation*}
V_i(x) = \frac 3 2 g_{ijk} x_j x_k + \frac 1 2 g_{ijk} g_{jlm} x_k x_l x_m
\end{equation*}

\begin{equation*}
V_{ij}(x) = 3 g_{ijk} x_k + \frac 1 2 \left( g_{ijk} g_{klm} x_l x_m + 2g_{ikl} g_{jkm} x_l x_m \right)
\end{equation*}

\begin{equation*}
V_{ijk}(x) = 3 g_{ijk} + g_{ijk} g_{klm} x_m + 2g_{ikl} g_{jkm} x_m
\end{equation*}

\begin{equation*}
V_{ijkl}(x) = g_{ijm}g_{klm} + 2g_{ikm} g_{jlm} x_m = 3g_{ijm}g_{klm}
\end{equation*}

At this point I should have all necessary tools to write down the Feynman rules and proceed with the diagrammatic interpretation. However I am struggling to see how I can proceed, in an analogous way Osborn did in section 1.4

Any guidance is much appreciated.

Thank you

 

[mark726]

Hello there,

Thank you for sharing your approach and progress so far. It seems like you have a good understanding of the mathematical calculations involved in solving this problem. However, as you mentioned, the next step would be to interpret these results in terms of Feynman rules and diagrams.

To do this, you can start by identifying the vertices in the potential function and assigning them appropriate factors. For example, the term $g_{ijk}$ can be interpreted as a vertex with three external legs corresponding to the fields $\theta_i, \bar{\theta}_j$ and $x_k$. Similarly, the term $g_{ijk}g_{jlm}$ can be interpreted as a vertex with four external legs corresponding to the fields $\theta_i, \bar{\theta}_j, x_k$ and $x_l$. You can continue this process for all terms in the potential, assigning the appropriate factors to each vertex.

Once you have identified the vertices, you can then draw the corresponding Feynman diagrams by connecting the external legs with propagators, which in this case would be the fields $x_i$. The factors assigned to each vertex will determine the strength of the interaction in the diagram.

I hope this helps guide you in the right direction. If you have any further questions, please don't hesitate to ask. Good luck!