- #1
Eric08
- 3
- 0
Homework Statement
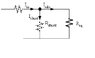
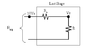
Design a resistive ladder so that, when driven by a 1000V source, yields the voltages 100v, 10v, 1v, 100mv, 10mv, and 1 mv under the following constraints
(A) the equivalent resistance seen by the source must be 1 Mega-ohm.
(B) the current entering each node must split between the subsequent series and shunt the resistances in a 3 to 1 ratio.
Homework Equations
The Attempt at a Solution
I attempted to start the design of this ladder but I am not sure how to choose my resistances so that the equivalent is the 1 Mega-ohm. Also, what do they mean in part B of this question by shunting the resistances into a 3 to 1 ratio?