- #1
SpY]
- 65
- 0
Hi everyone, I just started an introductory course in astronomy and we've covered co-ordinate systems on the celestial sphere. I haven't seen any threads like these so I apologize if it's in the wrong section.
In this very crude drawing of the northern celestial sphere, the observer is situated at a latitude θ North, corresponding to the altitude of the North celestial pole. Running from North to South is the celestial meridian, and perpendicular to that running from East to West is the celestial equator.
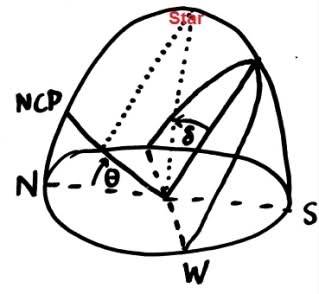
Now for a star that was on the celestial equator (declination zero), the total visible hour angle would be 12 hours - if the sidereal time was 0:00 then it would be 6:00 on the East point and 18:00 on the West point of the horizon. These are the times of starrise/starset (or sunrise/sunset for the sun).
My question is that if a star (or the sun at a time of the year) had a declination δ North of the celestial equator, how can you find the rising and setting times? All I have is that for δ=0, the the visible hour angle of the star is 12h; and for δ=90-θ North the star becomes circumpolar and 24h are visible.
In this very crude drawing of the northern celestial sphere, the observer is situated at a latitude θ North, corresponding to the altitude of the North celestial pole. Running from North to South is the celestial meridian, and perpendicular to that running from East to West is the celestial equator.
Now for a star that was on the celestial equator (declination zero), the total visible hour angle would be 12 hours - if the sidereal time was 0:00 then it would be 6:00 on the East point and 18:00 on the West point of the horizon. These are the times of starrise/starset (or sunrise/sunset for the sun).
My question is that if a star (or the sun at a time of the year) had a declination δ North of the celestial equator, how can you find the rising and setting times? All I have is that for δ=0, the the visible hour angle of the star is 12h; and for δ=90-θ North the star becomes circumpolar and 24h are visible.