- #1
amcavoy
- 665
- 0
I have the following problem:
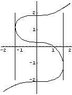
[tex]y'=\frac{3x^{2}}{3y^{2}-4};\quad y(1)=0[/tex]
I solved this, and came up with [itex]y^{3}-4y-x^{3}=-1[/itex]
My problem lies in finding the interval of definition. From the original DE, it is clear that [itex]|y|\neq \frac{2\sqrt{3}}{3}[/itex]. Then, after plugging that in for y and solving for what x can't be, I come up with:
[tex]\left|x^{3}-1\right|\neq \frac{16\sqrt{3}}{9}[/tex]
...however, my reasoning doesn't seem to work here. Apparently, the answer is:
[tex]\left|x^{3}-1\right|<\frac{16\sqrt{3}}{3}[/tex]
Can someone help me out here?
Thanks a lot.
[tex]y'=\frac{3x^{2}}{3y^{2}-4};\quad y(1)=0[/tex]
I solved this, and came up with [itex]y^{3}-4y-x^{3}=-1[/itex]
My problem lies in finding the interval of definition. From the original DE, it is clear that [itex]|y|\neq \frac{2\sqrt{3}}{3}[/itex]. Then, after plugging that in for y and solving for what x can't be, I come up with:
[tex]\left|x^{3}-1\right|\neq \frac{16\sqrt{3}}{9}[/tex]
...however, my reasoning doesn't seem to work here. Apparently, the answer is:
[tex]\left|x^{3}-1\right|<\frac{16\sqrt{3}}{3}[/tex]
Can someone help me out here?
Thanks a lot.
Last edited: