- #1
DethRose
- 101
- 0
Digital Electronics Boolean Reduction! Help Please
Ok i need to figure out how to reduce this I've been working on it for 2 days straight and can't figure it out...please help...its due tommorow :uhh:
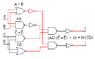
[tex](ab)[/tex][tex]([/tex][tex]\overline c + \overline d[/tex][tex])[/tex][tex]+[/tex][tex](a+b)[/tex][tex]([/tex][tex]\overline c \overline d)[/tex]
Ok i need to figure out how to reduce this I've been working on it for 2 days straight and can't figure it out...please help...its due tommorow :uhh:

[tex](ab)[/tex][tex]([/tex][tex]\overline c + \overline d[/tex][tex])[/tex][tex]+[/tex][tex](a+b)[/tex][tex]([/tex][tex]\overline c \overline d)[/tex]